
【題目】如圖,已知拋物線![]() 的頂點坐標為E(1,0),與
的頂點坐標為E(1,0),與![]() 軸的交點坐標為(0,1).
軸的交點坐標為(0,1).
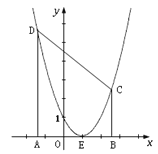

(1)求該拋物線的函數關系式.
(2)A、B是![]() 軸上兩個動點,且A、B間的距離為AB=4,A在B的左邊,過A作AD⊥
軸上兩個動點,且A、B間的距離為AB=4,A在B的左邊,過A作AD⊥![]() 軸交拋物線于D,
軸交拋物線于D,
過B作BC⊥![]() 軸交拋物線于C. 設A點的坐標為(
軸交拋物線于C. 設A點的坐標為(![]() ,0),四邊形ABCD的面積為S.
,0),四邊形ABCD的面積為S.
① 求S與![]() 之間的函數關系式.
之間的函數關系式.
② 求四邊形ABCD的最小面積,此時四邊形ABCD是什么四邊形?
③ 當四邊形ABCD面積最小時,在對角線BD上是否存在這樣的點P,使得△PAE的周長最小,若存在,請求出點P的坐標及這時△PAE的周長;若不存在,說明理由.
【答案】(1)![]() (2)①
(2)①![]() ②四邊形ABCD是正方形③2+
②四邊形ABCD是正方形③2+![]()
【解析】試題分析:(1)先設拋物線的頂點式,然后把點(0,1)代入拋物線,可以求出拋物線的解析式.(2)①因為點A的坐標為(t,0),AB=4,所以點B的坐標為(t+4,0),分別把A,B兩點的坐標代入拋物線得到C,D兩點的坐標,得到線段AD和BC的長,可以用含t的式子表示直角梯形ABCD的面積.②根據①得到S關于t的二次函數,利用二次函數的性質,可以求出面積最小時t的值,并確定此時四邊形的形狀.③當四邊形ABCD的面積最小時,ABCD是正方形,點A點C關于BD對稱,根據兩點之間線段最短,得到CE與BD的交點就是點P,然后求出△PAE的周長.
試題解析: (1)∵ 拋物線![]() 頂點為F(1,0)
頂點為F(1,0)
∴ ![]()
∵ 該拋線經過點E(0,1)
∴ ![]()
∴ ![]()
∴ ![]() ,
,
即所求拋物線的函數關系式為![]() .
.
(2)① ∵ A點的坐標為(![]() ,0), AB=4,且點C、D在拋物線上,
,0), AB=4,且點C、D在拋物線上,
∴ B、C、D點的坐標分別為(![]() +4,0),(
+4,0),(![]() +4, (
+4, (![]() +3)2),(
+3)2),(![]() ,(
,(![]() -1)2).
-1)2).
∴ ![]()
② ![]() .
.
∴ 當![]() =-1時,四邊形ABCD的最小面積為16,
=-1時,四邊形ABCD的最小面積為16,
此時AD=BC=AB=DC=4,四邊形ABCD是正方形.
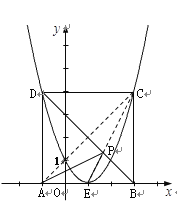
③ 當四邊形ABCD的面積最小時,四邊形ABCD是正方形,其對角線BD上存在點P, 使得ΔPAE的周長最小.
∵AE=4(定值),
∴要使ΔPAE的周長最小,只需PA+PE最小.
∵此時四邊形BCD是正方形,點A與點C關于BD所在直線對稱,
∴由幾何知識可知,P是直線CE與正方形ABCD對角線BD的交點.
∵點E、B、C、D的坐標分別為(1,0)(3,0)(3,4)(-1,4)
∴直線BD,EC的函數關系式分別為:y=-x+3, y=2x-2.
∴ P(![]() ,
,![]() )
)
在Rt△CEB中,CE=![]() ,
,
∴△PAE的最小周長=AE+AP+PE=AE+CP+PE=AE+CE=2+![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】下列命題中,真命題是( )
A. 對角線相等且互相垂直的四邊形是菱形 B. 有一條對角線平分對角的四邊形是菱形
C. 菱形是對角線互相垂直平分的四邊形 D. 菱形的對角線相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2+bx+c的圖象與直線y=x+1相交于點A(-1,m)和點B(n,5).

(1)求該二次函數的關系式;
(2)在給定的平面直角坐標系中,畫出這兩個函數的大致圖象;
(3)結合圖象直接寫出x2+bx+c>x+2時x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC內有一點D,AD=5,BD=6,CD=4,將△ABD繞A點逆時針旋轉,使AB與AC重合,點D旋轉至點E,則∠CDE的正切值為 ( )
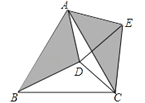
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩校參加區教育局舉辦的學生英語口語競賽,兩校參賽人數相同.比賽結束后,發現參賽學生成績分別為7分、8分、9分、10分(滿分為10分).
依據統計數據繪制了如下尚不完整的統計圖表.

(1)在圖1中,“7分”所在扇形的圓心角等于 度;將圖2的統計圖補充完整;
(2)經計算,乙校的平均分是8.3分,中位數是8分,請寫出甲校的平均分、中位數,并從平均分和中位數的角度分析哪所學校的成績較好;
(3)如果該教育局要組織8人的代表隊參加市級團體賽,為便于管理,決定從這兩所學校中的一所挑選參賽選手,請你分析,應選哪所學校合適?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】森林公園的門票價格規定如下表:
購票人數 | 1~50人 | 51~100人 | 100人以上 |
每人門票價 | 13元 | 11元 | 9元 |
某校初一(5)(6)兩個班共104人去游森林公園,其中(5)班人數較少,不到50人;(6)班人數較多,(6)班人數多于50人且少于100人.經估算,如果兩班都是以班為單位分別購票則一共應付1240元;
(1)求這兩個班各有多少名學生?
(2)團體購票與單獨購票相比較,兩個班各節約了多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,以O為圓心,適當長為半徑畫弧,交x軸于點M,交y軸于點N,再分別以點M、N為圓心,大于![]() MN的長為半徑畫弧,兩弧在第二象限交于點P.若點P的坐標為(2a,b+1),則a與b的數量關系為( )
MN的長為半徑畫弧,兩弧在第二象限交于點P.若點P的坐標為(2a,b+1),則a與b的數量關系為( )
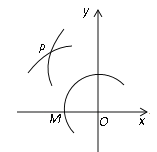
A. a=b B. 2a-b=1 C. 2a+b=-1 D. 2a+b=1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com