
【題目】“端午節”是我國的傳統佳節,歷來有吃“粽子”的習俗.我市某食品加工廠,擁有A、B兩條粽子加工生產線.原計劃A生產線每小時加工粽子個數是B生產線每小時加工粽子個數的![]() .
.
(1)若A生產線加工4000個粽子所用時間與B生產線加工4000個粽子所用時間之和恰好為18小時,則原計劃A、B生產線每小時加工粽子各是多少個?
(2)在(1)的條件下,原計劃A、B生產線每天均加工a小時,由于受其他原因影響,在實際加工過程中,A生產線每小時比原計劃少加工100個,B生產線每小時比原計劃少加工50個.為了盡快將粽子投放到市場,A生產線每天比原計劃多加工3小時,B生產線每天比原計劃多加工![]() a小時.這樣每天加工的粽子不少于6300個,求a的最小值.
a小時.這樣每天加工的粽子不少于6300個,求a的最小值.
【答案】(1)A、B生產線每小時加工粽子各是400、500個;(2)a的最小值為6.
【解析】
(1)首先根據“原計劃A生產線每小時加工粽子個數是B生產線每小時加工粽子個數的![]() ”設原計劃B生產線每小時加工粽子5x個,則原計劃A生產線每小時加工粽子4x個,再根據“A生產線加工4000個粽子所用時間與B生產線加工4000個粽子所用時間之和恰好為18小時”列出方程,再解即可;
”設原計劃B生產線每小時加工粽子5x個,則原計劃A生產線每小時加工粽子4x個,再根據“A生產線加工4000個粽子所用時間與B生產線加工4000個粽子所用時間之和恰好為18小時”列出方程,再解即可;
(2)根據題意可得A加工速度為每小時300個,B的加工速度為每小時450個,根據題意可得A的加工時間為(a+3)小時,B的加工時間為(a+![]() a)小時,再根據每天加工的粽子不少于6300個可得不等式(400-100)(a+3)+(500-50)(a+
a)小時,再根據每天加工的粽子不少于6300個可得不等式(400-100)(a+3)+(500-50)(a+![]() a)≥6300,再解不等式可得a的取值范圍,然后可確定答案.
a)≥6300,再解不等式可得a的取值范圍,然后可確定答案.
(1)設原計劃B生產線每小時加工粽子5x個,則原計劃A生產線每小時加工粽子4x個,
根據題意得![]() ,
,
∴x=100,
經檢驗x=100為原分式方程的解
∴4x=4×100=400,5x=5×100=500,
答:原計劃A、B生產線每小時加工粽子各是400、500個;
(2)由題意得:(400﹣100)(a+3)+(500﹣50)(a+![]() a)≥6300,
a)≥6300,
解得:a≥6,
∴a的最小值為6.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,點C的坐標為(4,﹣1).
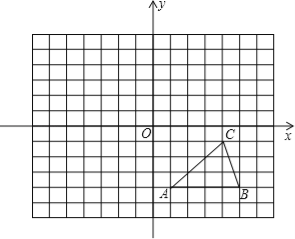
(1)把△ABC向上平移5個單位后得到對應的△A1B1C1,畫出△A1B1C1,并寫出C1的坐標;
(2)以原點O為對稱中心,再畫出與△A1B1C1關于原點O對稱的△A2B2C2,并寫出點C2的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面的統計圖表示某體校射擊隊甲、乙兩名隊員射擊比賽的成績,根據統計圖中的信息,下列結論正確的是( )
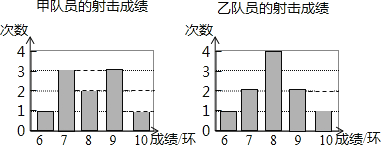
A. 甲隊員成績的平均數比乙隊員的大
B. 乙隊員成績的平均數比甲隊員的大
C. 甲隊員成績的中位數比乙隊員的大
D. 甲隊員成績的方差比乙隊員的大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在邊長為1的小正方形網格中,△AOB的頂點均在格點上.
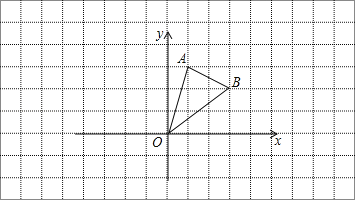
(1)B點關于y軸的對稱點坐標為 ;
(2)將△AOB向左平移3個單位長度,再向上平移2個單位長度得到△A1O1B1,請畫出△A1O1B1;
(3)在(2)的條件下,△AOB邊AB上有一點P的坐標為(a,b),則平移后對應點P1的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數![]() 與反比例函數
與反比例函數![]() 的圖像相交于點
的圖像相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() .
.
(1)填空:![]() 的值為 ,
的值為 ,![]() 的值為 ;
的值為 ;
(2)觀察反比函數![]() 的圖像,當
的圖像,當![]() 時,請直接寫出自變量
時,請直接寫出自變量![]() 的取值范圍;
的取值范圍;
(3)以![]() 為邊作菱形
為邊作菱形![]() ,使點
,使點![]() 在
在![]() 軸負半軸上,點
軸負半軸上,點![]() 在第二象限內,求點
在第二象限內,求點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(12分)如圖1所示,將一個邊長為2的正方形ABCD和一個長為2、寬為1的矩形CEFD拼在一起,構成一個大的長方形ABEF.現將小長方形CEFD繞點C順時針旋轉至CE′F′D,旋轉角為![]() .
.
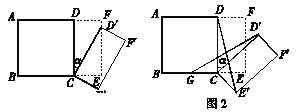
(1)當點D′恰好落在EF邊上時,則旋轉角α的值為________度;
(2)如圖2,G為BC中點,且0°<α<90°,求證:GD′=E′D;
(3)小長方形CEFD繞點C順時針旋轉一周的過程中,是否存在旋轉角α,使△DCD′與△CBD′全等?若能,直接寫出旋轉角α的值;若不能,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com