
【題目】如圖,![]() 中,
中,![]() .
.![]() . 將
. 將![]() 繞點
繞點![]() 順時針旋轉60°到點
順時針旋轉60°到點![]() ,點
,點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,連接
對稱,連接![]() ,
,![]() ,
,![]() .
.
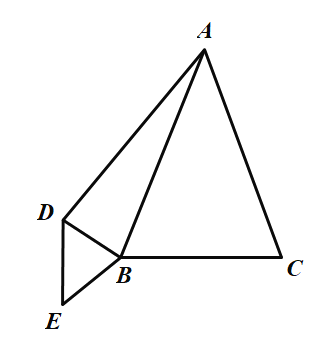
(1)依題意補全圖形:
(2)判斷![]() 的形狀,并證明你的結論;
的形狀,并證明你的結論;
(3)請問在直線![]() 上是否存在點
上是否存在點![]() .使得
.使得![]() 恒成立若存在,請用文字描述出點
恒成立若存在,請用文字描述出點![]() 的準確位置,并畫圖證明;若不存在,請說明理由.
的準確位置,并畫圖證明;若不存在,請說明理由.
【答案】(1)圖見解析;(2)![]() 是等邊三角形,理由見解析;(3)存在,點P是在將
是等邊三角形,理由見解析;(3)存在,點P是在將![]() 繞點C順時針旋轉60°得到
繞點C順時針旋轉60°得到![]() ,直線
,直線![]() 與直線
與直線![]() 的交點,圖和理由見解析.
的交點,圖和理由見解析.
【解析】
(1)根據題意畫出圖形即可;
(2)首先利用垂直平分線的性質得出![]() ,然后根據旋轉的性質有
,然后根據旋轉的性質有![]() 是等邊三角形,然后利用等邊三角形,等腰三角形的性質和三角形內角和定理得出
是等邊三角形,然后利用等邊三角形,等腰三角形的性質和三角形內角和定理得出![]() ,從而可證
,從而可證![]() ,則有
,則有![]() ,從而可證
,從而可證![]() 是等邊三角形;
是等邊三角形;
(3)將![]() 繞點C順時針旋轉60°得到
繞點C順時針旋轉60°得到![]() ,延長
,延長![]() 交直線
交直線![]() 于點P,連接
于點P,連接![]() ,先利用旋轉的性質得出
,先利用旋轉的性質得出![]() 是等邊三角形,然后通過等量代換得出
是等邊三角形,然后通過等量代換得出![]() ,從而可證
,從而可證![]() ,則
,則![]() ,再通過等腰三角形的性質和角度之間的關系得出
,再通過等腰三角形的性質和角度之間的關系得出![]() ,又因為
,又因為![]() ,
,![]() ,則有
,則有![]() .
.
(1)如圖,
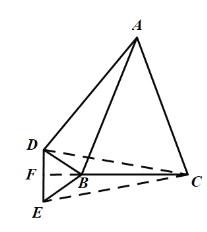
(2)![]() 是等邊三角形,理由如下:
是等邊三角形,理由如下:
連接CD,CE,延長CB交DE于點F,
∵點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱,
對稱,
∴CF垂直平分DE,
∴![]() .
.
由旋轉可知,![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,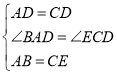
![]()
![]() ,
,
![]() ,
,
∴![]() 是等邊三角形;
是等邊三角形;
(3)存在,點P是在將![]() 繞點C順時針旋轉60°得到
繞點C順時針旋轉60°得到![]() ,直線
,直線![]() 與直線
與直線![]() 的交點,理由如下:
的交點,理由如下:
將![]() 繞點C順時針旋轉60°得到
繞點C順時針旋轉60°得到![]() ,延長
,延長![]() 交直線
交直線![]() 于點P,連接
于點P,連接![]() ,如圖,
,如圖,
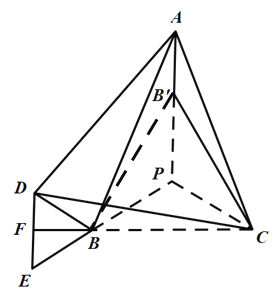
由(2)可知![]() 是等邊三角形,
是等邊三角形,
![]() ,
,
![]() ,
,
![]() .
.
由旋轉可知,![]() ,
,
∴![]() 是等邊三角形,
是等邊三角形,![]() ,
,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]()
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,![]()
![]() ,
,
∴直線BE上存在一點P,使得![]() ,點P是在將
,點P是在將![]() 繞點C順時針旋轉60°得到
繞點C順時針旋轉60°得到![]() ,直線
,直線![]() 與直線
與直線![]() 的交點.
的交點.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】為了解某種電動汽車的性能,對這種電動汽車進行了抽檢,將一次充電后行駛的里程數分為A,B,C,D四個等級,其中相應等級的里程依次為200千米,210千米,220千米,230千米,獲得如下不完整的統計圖,根據信息解答下列問題:

(1)問這次被抽檢的電動汽車共有幾輛?并補全條形統計圖:
(2)求電動汽車一次充電后行駛里程數的中位數、眾數:
(3)一次充電后行駛里程數220千米以上(含220千米)為優質等級,若全市有這種電動汽車1200輛,估計優質等級的電動汽車約為多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,二次函數y=x2+2x﹣3的圖象如圖所示,點A(x1,y1),B(x2,y2)是該二次函數圖象上的兩點,其中﹣3≤x1<x2≤0,則下列結論正確的是( )
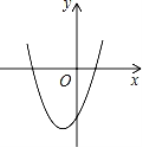
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2﹣4與x軸交于點A,B(點A位于點B的左側),C為頂點,直線y=x+m經過點A,與y軸交于點D.
(1)求線段AD的長;
(2)沿直線AD方向平移該拋物線得到一條新拋物線,設新拋物線的頂點為C',若點C'在反比例函數![]() (x<0)的圖象上.求新拋物線對應的函數表達式.
(x<0)的圖象上.求新拋物線對應的函數表達式.
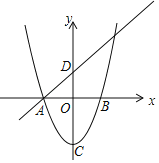
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小輝為了解市政府調整水價方案的社會反響,隨機訪問了自己居住在小區的部分居民,就“每月每戶的用水量”和“調價對用水行為改變”兩個問題進行調查,并把調查結果整理成下面的圖1,圖2.
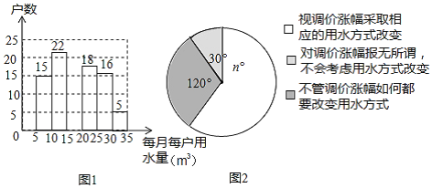
小輝發現每月每戶的用水量在![]() 之間,有7戶居民對用水價格調價漲幅抱無所謂,不用考慮用水方式的改變.根據小軍繪制的圖表和發現的信息,完成下列問題:
之間,有7戶居民對用水價格調價漲幅抱無所謂,不用考慮用水方式的改變.根據小軍繪制的圖表和發現的信息,完成下列問題:
(1)![]() ,小明調查了 戶居民,并補全圖1;
,小明調查了 戶居民,并補全圖1;
(2)每月每戶用水量的中位數落在 之間,眾數落在 之間;
(3)如果小明所在的小區有1200戶居民,請你估計“視調價漲幅采取相應的用水方式改變”的居民戶數多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
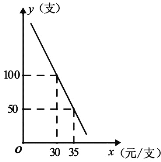
【題目】某網店專售一品牌牙膏,其成本為22元/支,銷售中發現,該商品每天的銷售量![]() (支)與銷售單價
(支)與銷售單價![]() (元/支)之間存在如圖所示的關系.
(元/支)之間存在如圖所示的關系.
(1)請求出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)該品牌牙膏銷售單價定為多少元時,每天銷售利潤最大?最大利潤是多少元?
(3)在武漢爆發“新型冠狀病毒”疫情期間,該網店店主決定從每天獲得的利潤中抽出100元捐贈給武漢,為了保證捐款后每天剩余的利潤不低于350元,在抗“新型冠狀病毒”疫情期間,市場監督管理局加大了對線上、線下商品銷售的執法力度,對商品售價超過成本價的20%的商家進行處罰,請你給該網店店主提供一個合理化的銷售單價范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
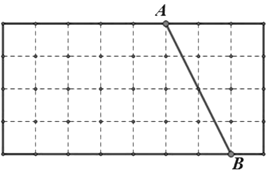
【題目】如圖,方格紙中的每個小正方形的邊長均為1,線段 AB的兩個端點均在小正方形的頂點上.
(1)在圖中畫出以AB為直角邊的Rt△ABC,點C在小正方形的頂點上,且Rt△ABC的面積為5;
(2)在(1)的條件下,畫出△BCD,點D在小正方形的頂點上,且tan∠CDB![]() ,連接AD,請直接寫出線段AD的長.
,連接AD,請直接寫出線段AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過坐標原點![]() 和
和![]() 軸上另一點
軸上另一點![]() ,頂點
,頂點![]() 的坐標為
的坐標為![]() .矩形
.矩形![]() 的頂點
的頂點![]() 與點O重合,AD、AB分別在x軸、y軸上,且AD=2,AB=3.
與點O重合,AD、AB分別在x軸、y軸上,且AD=2,AB=3.
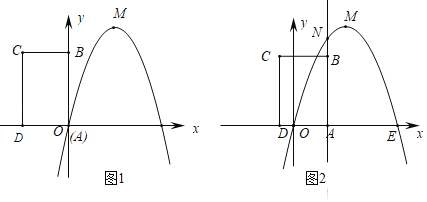
(1)求該拋物線所對應的函數關系式;
(2)將矩形![]() 以每秒
以每秒![]() 個單位長度的速度從圖1所示的位置沿
個單位長度的速度從圖1所示的位置沿![]() 軸的正方向勻速平行移動,同時一動點
軸的正方向勻速平行移動,同時一動點![]() 也以相同的速度從點
也以相同的速度從點![]() 出發向
出發向![]() 勻速移動,設它們運動的時間為
勻速移動,設它們運動的時間為![]() 秒
秒![]() ,直線
,直線![]() 與該拋物線的交點為
與該拋物線的交點為![]() (如圖2所示).
(如圖2所示).
①當![]() ,判斷點
,判斷點![]() 是否在直線
是否在直線![]() 上,并說明理由;
上,并說明理由;
②設P、N、C、D以為頂點的多邊形面積為![]() ,試問
,試問![]() 是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
是否存在最大值?若存在,求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現如今,“垃圾分類”意識已深入人心,垃圾一般可分為:可回收物、廚余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了兩袋垃圾.
(1)直接寫出甲所拿的垃圾恰好是“廚余垃圾”的概率;
(2)求乙所拿的兩袋垃圾不同類的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com