【題目】記
，則
的最小值為__________．
【答案】90
【解析】
根據題意可知
=|x-1|+|x-2|+|x-3|+…+|x-19|，由絕對值的意義以及數軸上兩點間的距離可知|x-a|表示x到a的距離，只有當x到1的距離等于x到19的距離時，式子取得最小值．據此進行求解即可得.
∵
，
∴=|x-1|+|x-2|+|x-3|+…+|x-19|，
由絕對值的意義以及數軸上兩點間的距離可知|x-a|表示x到a的距離，只有當x到1的距離等于x到19的距離時，式子取得最小值．
∴當x=
=10時，式子取得最小值，
此時，=|x-1|+|x-2|+|x-3|+…+|x-19|
=|10-1|+|10-2|+|10-3|+…+|10-9|+|10-10|+|10-11|+…+|10-18|+|10-19|
=9+8+7+…+1+0+1+2+…+8+9
=2×(1+2+3+…+9)
=2×45
=90，
故答案為：90.
三新快車金牌周周練系列答案科目：初中數學 來源： 題型：
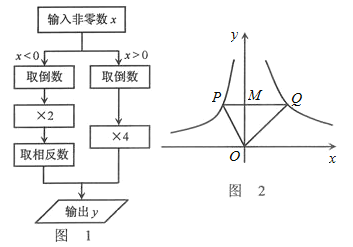
【題目】根據圖1所示的程序，得到了如圖y與x的函數圖像，若點M是y軸正半軸上任意一點，過點M作PQ∥x軸交圖像于點P、Q，連接OP、OQ．則以下結論：①x<0 時，y=
；②△OPQ的面積為定值；③x>0時，y隨x的增大而增大；④MQ=2PM⑤∠POQ可以等于90°．其中正確結論序號是（ ）
A.①②③B.②③④C.③④⑤D.②④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為鼓勵居民節約用電，某市采用價格調控手段達到省電目的.該市電費收費標準如下表(按月結算) :
每月用電量/度 | 電價/(元/度) |
不超過 |
|
超過 |
|
超過 |
|
解答下列問題:
（1）某居民
月份用電量為
度，請問該居民月應繳電費多少元？
（2）設某月的用電量為
度
，試寫出不同用電量范圍應繳的電費(用表示) .
（3）某居民月份繳電費元，求該居民月份的用電量.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了解學生“體育課外活動”的鍛煉效果，在期末結束時，隨機從學校1200名學生中抽取了部分學生的體育測試成績繪制了條形統計圖，請根據統計圖提供的信息，回答下列問題．
(1)這次抽樣調查共抽取了多少名學生的體育測試成績進行統計？
(2)隨機抽取的這部分學生中男生體育成績的眾數是多少？女生體育成績的中位數是多少？
(3)若將不低于40分的成績評為優秀，請估計這1200名學生中成績為優秀的學生大約是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在平面直角坐標系中，拋物線y＝x2－4x－5與x軸分別交于A、B（A在B的左邊），與y軸交于點C，直線AP與y軸正半軸交于點M，交拋物線于點P，直線AQ與y軸負半軸交于點N，交拋物線于點Q，且OM＝ON，過P、Q作直線l
(1) 探究與猜想：
① 取點M(0，1)，直接寫出直線l的解析式
取點M(0，2)，直接寫出直線l的解析式
② 猜想：
我們猜想直線l的解析式y＝kx＋b中，k總為定值，定值k為__________，請取M的縱坐標為n，驗證你的猜想
(2) 如圖2，連接BP、BQ．若△ABP的面積等于△ABQ的面積的3倍，試求出直線l的解析式
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】函數y=
是反比例函數．
（1）求m的值；
（2）指出該函數圖象所在的象限，在每個象限內，y隨x的增大如何變化？
（3）判斷點（
，2）是否在這個函數的圖象上．
查看答案和解析>>
科目：初中數學 來源： 題型：
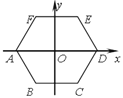
【題目】如圖，正六邊形 ABCDEF的中心與坐標原點O重合，其中A(-2，0)．將六邊形 ABCDEF繞原點O按順時針方向旋轉2018次，每次旋轉60°，則旋轉后點A的對應點A'的坐標是（ ）．
A. (1，
) B. (，1) C. (1，
) D. (-1，)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
