
【題目】觀察發現:如圖(1),![]() 是
是![]() 的外接圓,點
的外接圓,點![]() 是邊
是邊![]() 上的一點,且
上的一點,且![]() 是等邊三角形.
是等邊三角形.![]() 與
與![]() 交于點
交于點![]() ,以
,以![]() 為圓心、
為圓心、![]() 為半徑的圓交
為半徑的圓交![]() 于點
于點![]() ,連接
,連接![]() .
.
(1)![]() _____;
_____;
(2)線段![]() 、
、![]() 有何大小關系?證明你的猜想.
有何大小關系?證明你的猜想.
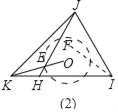
拓展應用:如圖(2),![]() 是等邊三角形,點
是等邊三角形,點![]() 是
是![]() 延長線上的一點.點
延長線上的一點.點![]() 是
是![]() 的外接圓圓心,
的外接圓圓心,![]() 與
與![]() 相交于點
相交于點![]() .如果等邊三角形
.如果等邊三角形![]() 的邊長為2,請直接寫出
的邊長為2,請直接寫出![]() 的最小值和此時
的最小值和此時![]() 的度數.
的度數.

【答案】(1)120°;(2)見解析;(3)拓展應用:![]() 的最小值為
的最小值為![]() ,此時
,此時![]() .
.
【解析】
(1)根據△ABC是等邊三角形,可得∠ACB=60°,根據圓周角定理可得∠AOD的度數.(2)根據內角和定理和等邊三角形的性質可得![]() ,進而得到
,進而得到![]() ,根據邊角邊對應相等可得
,根據邊角邊對應相等可得![]() ,則
,則![]() .
.
拓展應用:以![]() 為圓心,以
為圓心,以![]() 長為半徑作圓,交
長為半徑作圓,交![]() 于
于![]() ,連結
,連結![]() ,則
,則![]() .當
.當![]() 時
時![]() 最小,
最小,![]() 時,
時,![]() .
.
解:觀察發現:(1)∵△ABC是等邊三角形,
∴∠ACB=60°,
∴∠AOD=2∠ACB=120°
故答案為120°.
(2)結論:AE=CF.
理由如下:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
拓展應用:以![]() 為圓心,以
為圓心,以![]() 長為半徑作圓,交
長為半徑作圓,交![]() 于
于![]() ,連結
,連結![]() ,則由以上結論可得:
,則由以上結論可得:![]() .
.
當![]() 時
時![]() 最小,
最小,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值為
的最小值為![]() ,此時
,此時![]() .
.


科目:初中數學 來源: 題型:
【題目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),則稱△PQN為“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),則稱△PQN為“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等邊三角形,判斷△ABC是否為“差角三角形”,并說明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判斷△ABC是否為“差角三角形”,若是,請寫出所有的“差角”并說明理由;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖a,網格中的每一個正方形的邊長為1,△ABC為格點三角形,直線MN為格點直線(點A、B、C、M、N在小正方形的頂點上).

(1)僅用直尺在圖a中作出△ABC關于直線MN的對稱圖形△A′B′C′.
(2)如圖b,僅用直尺將網格中的格點三角形ABC的面積三等分,并將其中的一份用鉛筆涂成陰影.
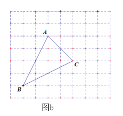
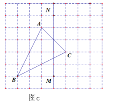
(3)如圖c,僅用直尺作三角形ABC的邊AC上的高,簡單說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
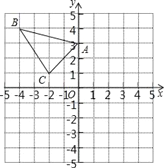
【題目】△ABC在直角坐標系內的位置如圖所示.
(1)分別寫出A、B、C的坐標;
(2)請在這個坐標系內畫出△A1B1C1,使△A1B1C1與△ABC關于y軸對稱,并寫出B1的坐標;
(3)請在這個坐標系內畫出△A2B2C2,使△A2B2C2與△ABC關于原點對稱,并寫出A2的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校準備購買若干臺A型電腦和B型打印機.如果購買1臺A型電腦,2臺B型打印機,一共需要花費5900元;如果購買2臺A型電腦,2臺B型打印機,一共需要花費9400元.
(1)求每臺A型電腦和每臺B型打印機的價格分別是多少元?
(2)如果學校購買A型電腦和B型打印機的預算費用不超過20000元,并且購買B型打印機的臺數要比購買A型電腦的臺數多1臺,那么該學校至多能購買多少臺B型打印機?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場為了吸引顧客,設置了兩種促銷方式.一種方式是:讓顧客通過轉轉盤獲得購物券.規定顧客每購買100元的商品,就能獲得一次轉轉盤的機會,如果轉盤停止后,指針正好對準100元、50元、20元的相應區域,那么顧客就可以分別獲得100元、50元、20元購物券,憑購物券可以在該商場繼續購物;如果指針對準其他區域,那么就不能獲得購物券.另一種方式是:不轉轉盤,顧客每購買100元的商品,可直接獲得10元購物券.據統計,一天中共有1 000人次選擇了轉轉盤的方式,其中指針落在100元、50元、20元的次數分別為50次、100次、200次.
(1)指針落在不獲獎區域的概率約是多少?
(2)通過計算說明選擇哪種方式更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將長方形紙片ABCD對折后再展開,得到折痕EF,M是BC上一點,沿著AM再次折疊紙片,使得點B恰好落在折痕EF上的點B′處,連接AB′、BB′.

判斷△AB′B的形狀為 ;
若P為線段EF上一動點,當PB+PM最小時,請描述點P的位置為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,然后回答問題 .
已知 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….,當
,….,當![]() 為大于1的奇數時,
為大于1的奇數時,![]() ;當
;當![]() 為大于1的偶數時,
為大于1的偶數時,![]() .
.
(1)求![]() ;(用含
;(用含![]() 的代數式表示)
的代數式表示)
(2)直接寫出![]() ;(用含
;(用含![]() 的代數式表示)
的代數式表示)
(3)計算:![]() = .
= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com