
【題目】如圖,四邊形ABCD中,∠B=90°,AB=BC=3 ![]() ,CD=8,AD=10.
,CD=8,AD=10. 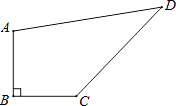
(1)求∠BCD的度數.
(2)求四邊形ABCD的面積.
【答案】
(1)解:連接AC,

在Rt△ABC中,∠B=90°,AB=BC=3 ![]() ,
,
根據勾股定理得:AC= ![]() =6,∠ACB=45°,
=6,∠ACB=45°,
∵CD=8,AD=10,
∴AD2=AC2+CD2,
∴△ACD為直角三角形,即∠ACD=90°,
則∠BCD=∠ACB+∠ACD=135°;
(2)解:根據題意得:S四邊形ABCD=S△ABC+S△ACD= ![]() ×3
×3 ![]() ×3
×3 ![]() +
+ ![]() ×6×8=9+24=33
×6×8=9+24=33
【解析】(1)連接AC,在直角三角形ABC中,利用勾股定理求出AC的長,再由CD與AD的長,利用勾股定理的逆定理判斷得到三角形ACD為直角三角形,再由等腰直角三角形的性質,根據∠BCD=∠ACB+∠ACD即可求出;(2)四邊形ABCD面積=三角形ABC面積+三角形ACD面積,求出即可.
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對勾股定理的逆定理的理解,了解如果三角形的三邊長a、b、c有下面關系:a2+b2=c2,那么這個三角形是直角三角形.


科目:初中數學 來源: 題型:
【題目】大美山水“硒都恩施”是一張亮麗的名片,八方游客慕名而來,今年“五一”期間,恩施州共接待游客1450000人,將1450000用科學記數法表示為( )
A.0.145×106
B.14.5×105
C.1.45×105
D.1.45×106
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個長方形運動場被分隔成A,B,A,B,C共5個區,A區是邊長為a m的正方形,C區是邊長為c m的正方形.
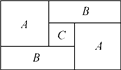
(1)列式表示每個B區長方形場地的周長,并將式子化簡;
(2)列式表示整個長方形運動場的周長,并將式子化簡;
(3)如果a=40,c=10,求整個長方形運動場的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2011年3月11日13時46分日本發生了9.0級大地震,伴隨著就是海嘯。山坡上有一棵與水平面垂直的大樹, 海嘯過后,大樹被刮傾斜后折斷倒在山坡上,樹的頂部恰好接觸到坡面(如圖所示)。已知山坡的坡角∠AEF=23°,量得樹干的傾斜角為∠BAC=38°,大樹被折斷部分和坡面所成的角∠ADC=60°,AD=4m。
(1)求∠DAC的度數;
(2)求這棵大樹折斷前AB的高?(結果精確到個位,參考數據: ![]() ).
).
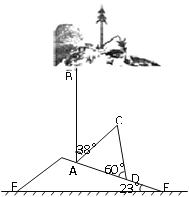
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列信息;據報道,全世界受到威脅的動物種類數如下表所示.請你按照下面要求回答問題:
全世界受到威脅的動物種類數 | ||||
動物分類 | 哺乳類 | 鳥類 | 爬行類 | 兩棲類 |
受到威脅的種類數(種) | 約1100 | 約1100 | 約300 | 約100 |
(1)制作適當的統計圖表示表中的數據,你選擇的統計圖是____________________;
(2)通過學習本題,請你寫一句20字左右的感想.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示是10×8的網格,網格中每個小正方形的邊長均為1,A、B兩點在小正方形的頂點上,使以A、B、C為頂點的三角形分別滿足以下要求: 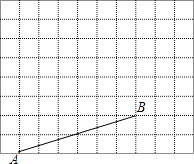
(1)請在圖中取一點C(點C必須在小正方形的頂點上),使△ABC為鈍角等腰三角形;
(2)通過計算,直接寫出△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀下面的文字,然后解答問題.
大家知道![]() 是無理數,而無理數是無限不循環小數,因此
是無理數,而無理數是無限不循環小數,因此![]() 的小數部分我們不可能全部寫出來,于是小明用
的小數部分我們不可能全部寫出來,于是小明用![]() ﹣1表示
﹣1表示![]() 的小數部分,你同意小明的表示方法嗎?事實上,小明的表示方法是有道理的,因為
的小數部分,你同意小明的表示方法嗎?事實上,小明的表示方法是有道理的,因為![]() 的整數部分是1,將這個數減去其整數部分,差就是小數部分.
的整數部分是1,將這個數減去其整數部分,差就是小數部分.
由此我們還可以得到一個真命題:如果![]() =x+y,其中x是整數,且0<y<1,那么x=1,y=
=x+y,其中x是整數,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
請解答下列問題:
(1)如果![]() =a+b,其中a是整數,且0<b<1,那么a= ,b= ;
=a+b,其中a是整數,且0<b<1,那么a= ,b= ;
(2)已知2+![]() =m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com