【題目】某校計劃購買一批學習筆記本，已知1本甲種筆記本和3本乙種筆記本共需26元；3本甲種筆記本和2本乙種筆記本共需29元．
（1）求購買一本甲種筆記本和一本乙種筆記本各需多少元；
（2）學校計劃購進這兩種筆記本共70本，并且甲種筆記本的數量不超過乙種筆記本數量的2倍，若設學校計劃購進甲種比價本x本．
①填寫下表：
甲種筆記本數量 | 10 |
|
乙種筆記本數量 |
| 30 |
所需總費用 |
|
|
②寫出購買這兩種筆記本所需要費用y（元）關于x的函數關系式；請設計出最省錢的購買方案，并說明理由
【答案】（1）購買一本甲種筆記本和一本乙種筆記本分別需要5元、7元；（2）①40，60，470，410，②y＝﹣2x+490，最省錢的購買方案是購買甲種筆記本46本，乙種筆記本24本
【解析】
（1）設購買一本甲種筆記本和一本乙種筆記本分別需要x元、y元，根據題意列出方程求解即可；
（2）①根據題意計算出各項的數據，并補全表格即可；②寫出購買這兩種筆記本所需要費用y（元）關于x的函數關系式，再根據一次函數的性質作答即可．
解：（1）設購買一本甲種筆記本和一本乙種筆記本分別需要x元、y元，
，
得
，
答：購買一本甲種筆記本和一本乙種筆記本分別需要5元、7元；
（2）①由題意可得，
當購買甲種筆記本數量為10本時，則購買的乙種筆記本數量是60本，所需的總費用為：10×5+60×7＝50+420＝470（元），
當購買乙種筆記本數量為30本時，則購買的甲種筆記本數量是40本，所需的總費用為：40×5+30×7＝200+210＝410（元），
故答案為：40、60、470、410；
②由題意可得，
y＝5x+7（70﹣x）＝5x+490﹣7x＝﹣2x+490，
∵甲種筆記本的數量不超過乙種筆記本數量的2倍，
∴x≤2（70﹣x），
解得，x≤46
，
∴當x＝46時，y取得最小值，此時y＝﹣2×46+490＝398，70﹣x＝24，
答：購買這兩種筆記本所需要費用y（元）關于x的函數關系式是y＝﹣2x+490，最省錢的購買方案是購買甲種筆記本46本，乙種筆記本24本．
名師指導期末沖刺卷系列答案
開心蛙口算題卡系列答案科目：初中數學 來源： 題型：
【題目】在我市“青山綠水”行動中，某村計劃對面積為3640
的山坡進行綠化，經投標由甲，乙兩個工程隊來完成．已知甲隊每天能完成綠化的面積是乙隊每天完能完成綠化的面積的2倍，如果兩隊各自獨立完成面積為400區域的綠化時，甲隊比乙隊少用4天．
（1）求甲、乙兩工程隊每天各能完成多少面積的綠化；
（2）若甲隊每天綠化費用是1.2萬元，乙隊每天綠化費用為0.5萬元，該村要使這次綠化的總費用不過40萬元，則至少應安排乙工程隊綠化多少天?
查看答案和解析>>
科目：初中數學 來源： 題型：
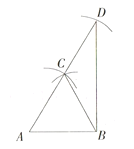
【題目】如圖，
，分別以點A、B為圓心，AB長為半徑畫圓弧，兩圓弧交于點C，再以點C為圓心，以AB長為半徑畫圓弧交AC的延長線于點D，連結BD、BC，則
的面積是___________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了促進學生多樣化發展，某校組織開展了社團活動，分別設置了體育類、藝術類、文學類及其它類社團（要求人人參與社團，每人只能選擇一項）．為了解學生喜愛哪種社團活動，學校做了一次抽樣調查．根據收集到的數據，繪制成如下兩幅不完整的統計圖，請根據圖中提供的信息，完成下列問題：
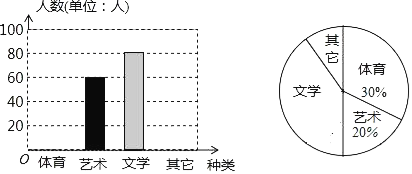
（1）此次共調查了多少人？
（2）求體育社團在扇形統計圖中所占圓心角的度數；
（3）請將條形統計圖補充完整；
（4）若該校有3000名學生，請估計喜歡文學類社團的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小元步行從家去火車站，走到 6 分鐘時，以同樣的速度回家取物品，然后從家乘出租車趕往火車站，結果比預計步行時間提前了3 分鐘．小元離家路程S(米)與時間t(分鐘)之間的函數圖象如圖，從家到火車站路程是( )
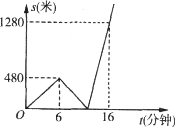
A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某區正在積極創建國家模范衛生城市，學校為了普及學生衛生健康知識，提高學生創衛意識，舉辦了創衛知識競賽，以下是從初一、初二兩個年級隨機抽取20名同學的測試成績進行調查分析，成績如下：
初一：75 88 93 65 78 94 89 68 95 50 89 88 89 89 77 95 87 88 92 91
初二：74 96 96 89 97 74 69 76 72 78 99 72 97 85 98 74 89 73 98 74
（1）整理、描述數據：
成績 |
|
|
|
|
|
初一（頻數） | 1 | 2 | 3 |
| 6 |
初二（頻數） | 0 | 1 | 9 | 3 | 7 |
（說明：成績90分及以上為優秀，80~90分為良好，60~80分為合格，60分以下不合格）
分析數據：
平均數 | 中位數 | 眾數 | |
初一 | 84 |
| 89 |
初二 | 84 | 81.5 |
|
請根據上述的數據，填空：
______；
______；
______；
（2）得出結論：
你認為哪個年級掌握創衛知識水平較好并說明理由．（至少從兩個不同的角度說明推斷的合理性）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】近段時間成都空氣質量明顯下降，市場上的空氣凈化器再次成為熱銷，某商店經銷--種空氣凈化器，每臺凈化器的成本價為
元，經過一段時間的銷售發現，每月的銷售量
臺與銷售單價
(元)的關系為
．
（1）該商店每月的利潤為
元，寫出利潤與銷售單價的函數關系式；
（2）若要使每月的利潤為
元，銷售單價應定為多少元？
（3）商店要求銷售單價不低于
元， 也不高于
元，那么該商店每月的最高利潤和最低利潤分別為多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
