
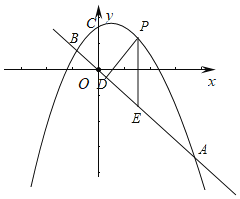
【題目】如圖,已知拋物線y=-x2+bx+c與直線y=-x的交點A、B的橫坐標分別為2和![]() .點P是直線上方拋物線上的一動點,過點P作PD⊥AB于點D,作PE⊥x軸交AB于點E.
.點P是直線上方拋物線上的一動點,過點P作PD⊥AB于點D,作PE⊥x軸交AB于點E.
(1)直接寫出點A、B的坐標;
(2)求拋物線的關系式;
(3)判斷△OBC形狀,并說明理由;
(4)設點P的橫坐標為n,線段PD的長為y,求y關于n的函數關系式;
(5)定義符號min{a,b)}的含義為:當a≥b時,min{a,b}=b;當a<b時,min{a,b}=a.如min{2,0}=0,min{-3,4}=-3.直接寫出min{-x2+bx+c,-x}的最大值.
【答案】(1)A(2-2),點B(-![]() ,
,![]() );(2)y=-x2+
);(2)y=-x2+![]() x+1;(3)△OBC是等腰直角三角形.理由見解析;(4)y=-
x+1;(3)△OBC是等腰直角三角形.理由見解析;(4)y=-![]() n2+
n2+![]() n+
n+![]() ;(5)min{-x2+
;(5)min{-x2+![]() x+1,-x}最大值為
x+1,-x}最大值為![]() .
.
【解析】
(1)A、B的橫坐標分別為2和-![]() ,代入解析式y=-x可得點A,點B的坐標;
,代入解析式y=-x可得點A,點B的坐標;
(2)用待定系數法可求解析式;
(3)由根據兩點距離公式可求OB,OC,BC的長度,可得BC=OB,根據勾股定理逆定理可判斷∠OBC=90°,即可求△OBC形狀;
(4)由點P的橫坐標為n,可求PE=-n2+![]() n+1,根據題意可求∠BOC=45°=∠PED,根據勾股定理可求PD=y=
n+1,根據題意可求∠BOC=45°=∠PED,根據勾股定理可求PD=y=![]() PE,即可求y關于n的函數關系式;
PE,即可求y關于n的函數關系式;
(5)分①-x2+![]() x+1≥-x時,②-x2+
x+1≥-x時,②-x2+![]() x+1<-x時,兩種情況討論,可求min{-x2+
x+1<-x時,兩種情況討論,可求min{-x2+![]() x+1,-x}最大值.
x+1,-x}最大值.
(1)∵A、B的橫坐標分別為2和![]() ,且點A,點B在直線y=-x上,
,且點A,點B在直線y=-x上,
∴A(2-2),點B(-![]() ,
,![]() ),
),
(2)∵拋物線y=-x2+bx+c經過點A,點B,
∴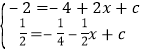 ,
,
解得:b=![]() ,c=1,
,c=1,
∴拋物線解析式y=-x2+![]() x+1,
x+1,
(3)△OBC是等腰直角三角形.
理由如下:∵拋物線y=-x2+![]() x+1與y軸交于點C,
x+1與y軸交于點C,
∴當x=0時,則y=1,
即點C坐標(0,1),
又∵點O(0,0),點B(-![]() ,
,![]() ),
),
∴OC=1,
OB=![]() =
=![]() ,
,
BC=![]() =
=![]() ,
,
∴OB=BC,
∵OB2+BC2=1,OC2=1,
∴OB2+BC2=OC2.
∴∠CBO=90°.
∴△OBC是等腰直角三角形.
(4)∵點P的橫坐標為n,
∴點P(n,-n2+![]() n+1),點E的坐標(n,-n),
n+1),點E的坐標(n,-n),
∴PE=-n2+![]() n+1-(-n)=-n2+
n+1-(-n)=-n2+![]() n+1,
n+1,
∵直線y=-x與x軸所成銳角為45°,
∴∠BOC=45°,
∵PE∥y軸,
∴∠PED=∠BOC=45°,且PD⊥AB,
∴PE=![]() PD,
PD,
∴y=![]() PE=
PE=![]() (-n2+
(-n2+![]() n+1)=-
n+1)=-![]() n2+
n2+![]() n+
n+![]() ,
,
(5)![]() ,
,
①-x2+![]() x+1≥-x時,min{-x2+
x+1≥-x時,min{-x2+![]() x+1,-x}=-x,
x+1,-x}=-x,
即-x2+![]() x+1≥-x,
x+1≥-x,
解得:-![]() ≤x≤2,
≤x≤2,
∴-2≤min{-x2+![]() x+1,-x}≤
x+1,-x}≤![]() ,
,
②-x2+![]() x+1<-x時,min{-x2+
x+1<-x時,min{-x2+![]() x+1,-x}=-x2+
x+1,-x}=-x2+![]() x+1,
x+1,
即-x2+![]() x+1<-x,
x+1<-x,
解得:x<-![]() 和x>2,
和x>2,
當x<-![]() 時,min{-x2+
時,min{-x2+![]() x+1,-x}<
x+1,-x}<![]() ,
,
當x>2時,min{-x2+![]() x+1,-x}<-2,
x+1,-x}<-2,
綜上所述:min{-x2+![]() x+1,-x}最大值為
x+1,-x}最大值為![]() .
.


科目:初中數學 來源: 題型:
【題目】某商場計劃從廠家購進甲、乙兩種不同型號的電視機,已知進價分別為:甲種每臺1500元,乙種每臺2100元.
(1)若商場同時購進這兩種不同型號的電視機50臺,金額不超過76000元,商場有幾種進貨方案,并寫出具體的進貨方案.
(2)在(1)的條件下,若商場銷售一臺甲、乙型號的電視機的銷售價分別為1650元、2300元,以上進貨方案中,哪種進貨方案獲利最多?最多為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC=∠DAF=90°,AB=AC,AD=AF,點D、E為BC邊上的兩點,且∠DAE=45°,連接EF、BF,則下列結論:①△AED≌△AEF ②△ABE∽△ACD,③BE+DC>DE④BE2+DC2=DE2,其中正確的有( )個

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店將每件進價為80元的某種商店按每件110元出售,每天可售出100件.該商店想通過降低售價、增加銷售量的方法來提高利潤.經市場調查,發現這種商品每件每降價5元,每天的銷售量可增加50件.設商品降價x元,每天銷售該商品獲得的利潤為y元.
(1)求y(元)關于x(元)的函數關系式,并寫出x的取值范圍.
(2)求當x取何值時y最大?并求出y的最大值.
(3)若要是每天銷售利潤為3750元,且盡可能最大的向顧客讓利,應將該商品降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春節期間,小麗一家乘坐高鐵前往某市旅游,計劃第二天租用新能源汽車自駕出游.
租車公司:按日收取固定租金80元,另外再按租車時間計費.
共享汽車:無固定租金,直接以租車時間(時)計費.
如圖是兩種租車方式所需費用y1(元)、y2(元)與租車時間x(時)之間的函數圖象,根據以上信息,回答下列問題:
(1)分別求出y1、y2與x的函數表達式;
(2)請你幫助小麗一家選擇合算的租車方案.
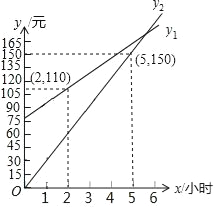
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦BC=2cm,F是弦BC的中點,∠ABC=60°.若動點E以2cm/s的速度從A點出發沿著A→B→A方向運動,設運動時間為t(s)(0≤t<3),連接EF,當△BEF是直角三角形時,t(s)的值為【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老張勻速開車從A市送貨到B市,途中汽車出現小故障,老張只能降速為原速的一半行駛等待B市的修車師傅小李前往修車,半小時后,小李與老張相遇,立馬開始修車,車修好后,老張又提速為原速的![]() 繼續開車送貨到B市,小李以原速返回B市,老張和小李距離B市的路程y(千米)與老張出發的時間x(小時)的函數圖象分別如圖所示(途中其它損耗時間忽略不計),則小李在返回到B市時,老張距B市______千米.
繼續開車送貨到B市,小李以原速返回B市,老張和小李距離B市的路程y(千米)與老張出發的時間x(小時)的函數圖象分別如圖所示(途中其它損耗時間忽略不計),則小李在返回到B市時,老張距B市______千米.
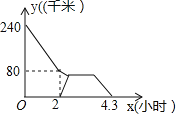
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 邊上的動點,點
邊上的動點,點![]() 從點
從點![]() 出發,沿邊
出發,沿邊![]() 向點
向點![]() 運動,當運動到點
運動,當運動到點![]() 時停止,若設點
時停止,若設點![]() 運動的時間為
運動的時間為![]() 秒,點
秒,點![]() 運動的速度為每秒2個單位長度.
運動的速度為每秒2個單位長度.
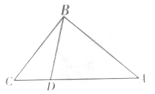

(1)當![]() 時,
時,![]() = ,
= ,![]() = ;
= ;
(2)求當![]() 為何值時,
為何值時,![]() 是直角三角形,說明理由;
是直角三角形,說明理由;
(3)求當![]() 為何值時,
為何值時,![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com