
【題目】如圖,已知反比例函數![]() 的圖像經過第二象限內的點A(-1,m),AB⊥x軸于點B,△AOB 的面積為2.若直線 y=ax+b經過點A,并且經過反比例函數的圖象上另一點C(n,-2).
的圖像經過第二象限內的點A(-1,m),AB⊥x軸于點B,△AOB 的面積為2.若直線 y=ax+b經過點A,并且經過反比例函數的圖象上另一點C(n,-2).
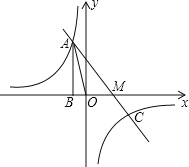
(1)求反比例函數![]() 與直線y=ax+b的解析式;
與直線y=ax+b的解析式;
(2)連接OC,求△AOC的面積;
(3)根據所給條件,直接寫出不等式![]() 的解集
的解集
【答案】(1)![]() ,
,![]() ;(2)S△AOC=3 ;(3)x≤-1 或0<x≤2.
;(2)S△AOC=3 ;(3)x≤-1 或0<x≤2.
【解析】分析:(1)根據點A的橫坐標與△AOB的面積求出AB的長度,從而得到點A的坐標,然后利用待定系數法求出反比例函數解析式,再利用反比例函數解析式求出點C的坐標,根據點A與點C的坐標利用待定系數法即可求出直線y=ax+b的解析式;
(2)先求出直線AC與x軸交點坐標,即點M的坐標,再根據S△AOC=S△AOM+S△MOC計算得到.
(3)根據圖象直接得出x的取值范圍.
詳解:
(1)∵點A(﹣1,m)在第二象限內,
∴AB=m,OB=1,
∴S△ABO=![]() ABBO=2,
ABBO=2,
即:![]() ×m×1=2,
×m×1=2,
解得m=4,
∴A (﹣1,4),
∵點A (﹣1,4),在反比例函數y=![]() 的圖象上,
的圖象上,
∴4=![]() ,
,
解得k=﹣4,
∴反比例函數為y=﹣![]() ,
,
又∵反比例函數y=﹣![]() 的圖象經過C(n,﹣2)
的圖象經過C(n,﹣2)
∴﹣2=![]() ,
,
解得n=2,
∴C (2,﹣2),
∵直線y=ax+b過點A (﹣1,4),C (2,﹣2)
∴![]() ,
,
解方程組得![]() ,
,
∴直線y=ax+b的解析式為y=﹣2x+2;
(2)y=﹣2x+2與x軸的交點M的坐標為:當y=0時,x=1,
所以點M(1,0),
S△AOC=S△AOM+S△MOC=![]()
(3)由圖象可知,當x≤-1 或0<x≤2時,ax+b![]() ,
,
故答案為x≤-1 或0<x≤2.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:初中數學 來源: 題型:
【題目】在一空曠場地上設計一落地為矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m長的繩子一端固定在B點處,小狗在不能進入小屋內的條件下活動,其可以活動的區域面積為S(m2).
①如圖1,若BC=4m,則S=m.
②如圖2,現考慮在(1)中的矩形ABCD小屋的右側以CD為邊拓展一正△CDE區域,使之變成落地為五邊形ABCED的小屋,其它條件不變.則在BC的變化過程中,當S取得最小值時,邊BC的長為m.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以AB為直徑的⊙O經過AC的中點D,DE⊥BC于點E. 
(1)求證:DE是⊙O的切線;
(2)當AB=4 ![]() ,∠C=30°時,求圖中陰影部分的面積(結果保留根號和π).
,∠C=30°時,求圖中陰影部分的面積(結果保留根號和π).
查看答案和解析>>
科目:初中數學 來源: 題型:
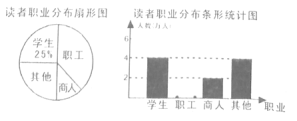
【題目】學習成為現代人的時尚,我,市有關部門統計了最近6個月到圖書館的讀者和職業分布情況,并做了下列兩個不完整的統計圖.請你根據圖中提供的信息,解答下列問題:
(l)求在統汁的這段時問內,到圖書館閱讀的總人次:
(2)請補全條形統汁圖,并求扇形統計圖中表示“商人”的扇形的圓心角度數;
(3)符5月份到圖書館的讀者共20000人次,估汁其中約有多少人次讀者是職工?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形網格中(網格中的每個小正方形邊長是1),△ABC的頂點均在格點上,請在所給的直角坐標系中解答下列問題:

⑴ 作出△![]() 繞點A逆時針旋轉90°的△AB1C1,再作出△AB1C1關于原點O成中心對稱的△A1B2C2.
繞點A逆時針旋轉90°的△AB1C1,再作出△AB1C1關于原點O成中心對稱的△A1B2C2.
(2)請直接寫出以A1、B2、C2為頂點的平行四邊形的第四個頂點D的坐標 .(寫出一個即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC,△EFG均是邊長為4的等邊三角形,點D是邊BC、EF的中點. (Ⅰ)如圖①,這兩個等邊三角形的高為;
(Ⅱ)如圖②,直線AG,FC相交于點M,當△EFG繞點D旋轉時,線段BM長的最小值是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,要建一個長方形養雞場,養雞場的一邊靠墻(墻長25米),另三邊用竹籬笆圍成,竹籬笆的長為40米,若要圍成的養雞場的面積為180平方米,求養雞場的寬各為多少米,設與墻平行的一邊長為x米. 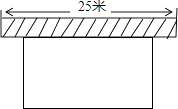
(1)填空:(用含x的代數式表示)另一邊長為米;
(2)列出方程,并求出問題的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,圖象過點(﹣1,0),對稱軸為直線x=2,系列結論:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若點A(﹣2,y1),點B( ![]() ,y2),點C(
,y2),點C( ![]() ,y2)在該函數圖象上,則y1<y3<y2;(5)若m≠2,則m(am+b)>2(2a+b),其中正確的結論有( )
,y2)在該函數圖象上,則y1<y3<y2;(5)若m≠2,則m(am+b)>2(2a+b),其中正確的結論有( ) 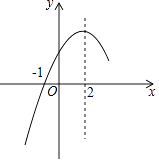
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①為一種平板電腦保護套的支架效果圖,AM固定于平板電腦背面,與可活動的MB、CB部分組成支架.平板電腦的下端N保持在保護套CB上,不考慮拐角處的弧度及平板電腦和保護套的厚度,繪制成圖②,其中AN表示平板電腦,M為AN上的定點,AN=CB=20cm,AM=8cm,MB=MN,我們把∠ANB叫做傾斜角,根據以上數據,判斷傾斜角能小于30°嗎?請說明理由.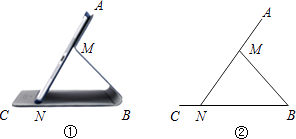
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com