
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 的中點,點
的中點,點![]() 是邊
是邊![]() 上一動點,沿
上一動點,沿![]() 所在直線把
所在直線把![]() 翻折到
翻折到![]() 的位置,若線段
的位置,若線段![]() 交
交![]() 于點
于點![]() ,且
,且![]() 為直角三角形,則
為直角三角形,則![]() 的長為______.
的長為______.
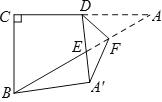
【答案】6或![]()
【解析】
由三角函數得出∠A=30°,由直角三角形的性質得出AB=2BC=8,由折疊的性質得出DA=DC=2![]() ,FA′=FA,∠DA′F=∠A=30°,設BF=x,則AF=8-x,FA′=8-x,①當∠BEA′=90°時,由三角函數得出AE=3,得出EF=3-(8-x)=x-5,由直角三角形的性質得出方程,解方程即可;
,FA′=FA,∠DA′F=∠A=30°,設BF=x,則AF=8-x,FA′=8-x,①當∠BEA′=90°時,由三角函數得出AE=3,得出EF=3-(8-x)=x-5,由直角三角形的性質得出方程,解方程即可;
②當∠BA'E=90°時,作FH⊥BA',交BA'的延長線于H,連接BD,證明Rt△BDA'≌Rt△BDC,得出BA′=BC=4,求出∠FA'H=60°,在Rt△BFH中,由勾股定理得出方程,解方程即可.
解:![]()
![]()
∴∠A=30°,
∴AB=2BC=8,
∵點D是AC的中點,沿DF所在直線把△ADF翻折到△A′DF的位置,線段A′D交AB于點E,
![]()
設BF=x,則AF=8-x,FA′=8-x,下面分兩種情況討論:
①當∠BEA′=90°時,在Rt△ADE中,![]()
![]()
∴EF=3-(8-x)=x-5,
在Rt△A'FE中,∵∠FA'E=30°,
∴FA'=2FE,即8-x=2(x-5),
解得x=6,即BF=6;
②當∠BA'E=90°時,作FH⊥BA',交BA'的延長線于H,連接BD,如圖所示: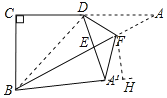
在Rt△BDA'和△BDC中![]()
∴Rt△BDA'≌Rt△BDC(HL),
∴BA′=BC=4,
∵∠BA'F=∠BA'E+∠FA'E=90°+30°=120°,
∴∠FA'H=60°,
在Rt△FHA'中,![]()
在Rt△BFH中,∵FH2+BH2=BF2,
![]()
解得:x= ![]() ,即BF=
,即BF= ![]() .
.
綜上所述,BF的長為6或![]() .
.
故答案為6或![]() .
.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖像經過點A(-1,0),并與反比例函數
的圖像經過點A(-1,0),并與反比例函數![]() (
(![]() )的圖像交于B(m,4)
)的圖像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB為一邊,在AB的左側作正方形![]() ,求C點坐標;
,求C點坐標;
(3)將正方形![]() 沿著
沿著![]() 軸的正方向,向右平移n個單位長度,得到正方形
軸的正方向,向右平移n個單位長度,得到正方形![]() ,線段
,線段![]() 的中點為點
的中點為點![]() ,若點
,若點![]() 和點
和點![]() 同時落在反比例函數
同時落在反比例函數![]() 的圖像上,求n的值.
的圖像上,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
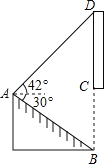
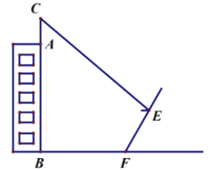
【題目】2021年世界園藝博覽會將在揚州棗林灣舉辦,有一塊棗林灣博覽會的直傳牌CD豎立在路邊,其中CB是支柱.小梅同學想計算出CD的長度.于是在A處測得支柱B處的俯角為30°.測得頂端D處的仰角為42°,同時測量出AB的長度是10m,BC的長度是6m.求宜傳牌CD的長度(結果保留小數點后一位).(參考數據:![]() ≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
≈1.73,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了美化環境,建設宜居成都,我市準備在一個廣場上種植甲、乙兩種花卉.經市場調查,甲種花卉的種植費用![]() (元)與種植面積
(元)與種植面積![]() 之間的函數關系如圖所示,乙種花卉的種植費用為每平方米100元.
之間的函數關系如圖所示,乙種花卉的種植費用為每平方米100元.

(1)直接寫出當![]() 和
和![]() 時,
時,![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)廣場上甲、乙兩種花卉的種植面積共![]() ,若甲種花卉的種植面積不少于
,若甲種花卉的種植面積不少于![]() ,且不超過乙種花卉種植面積的2倍,那么應該怎樣分配甲、乙兩種花卉的種植面積才能使種植費用最少?最少總費用為多少元?
,且不超過乙種花卉種植面積的2倍,那么應該怎樣分配甲、乙兩種花卉的種植面積才能使種植費用最少?最少總費用為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為構建“魅力雨花,和諧雨花,人文雨花”,規劃在圭塘河上修建一座觀光人行橋(如圖1),此工程由橋梁工程與橋上拱形工程組成,橋上拱形工程包含三組完全相同的拱形,觀光人行橋的正規圖如圖2所示,已知橋面上三組拱橋都為相同的拋物線![]() 的一部分,拱高(拋物線最高點到橋面的距離)為16米,三條拋物線依次與橋面AB相較于點A,C,D,B.
的一部分,拱高(拋物線最高點到橋面的距離)為16米,三條拋物線依次與橋面AB相較于點A,C,D,B.

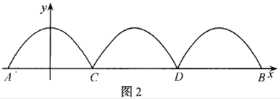
(1)求橋長AB;
(2)已知一組橋拱的造價為a萬元,橋面每米的平均造價為b萬元.若一組橋拱的造價為整個橋面造價的![]() ,這座觀光橋的總造價為504萬元,求a,b的值.
,這座觀光橋的總造價為504萬元,求a,b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校計劃購進甲、乙兩種規格的書架,經市場調查發現有線上和線下兩種購買方式,具體情況如下表:
規格 | 線下 | 線上 | ||
單價(元/個) | 運費(元/個) | 單價(元/個) | 運費(元/個) | |
甲 | 240 | 0 | 210 | 20 |
乙 | 300 | 0 | 250 | 30 |
(1)如果在線下購買甲、乙兩種書架共30個,花費8280元,求甲、乙兩種書架各購買了多少個?
(2)如果在線上購買甲、乙兩種書架共30個,且購買乙種書架的數量不少于甲種書架的3倍,請求出花費最少的購買方案及花費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為全面推進“三供一業”分離移交工作,甲、乙兩個工程隊承攬了某社區2400米的電路管道鋪設工程.已知甲隊每天鋪設管道的長度是乙隊每天鋪設管道長度的1.5倍,若兩隊各自獨立完成1200米的鋪設任務,則甲隊比乙隊少用10天.
(1)求甲、乙兩工程隊每天分別鋪設電路管道多少米;
(2)若甲隊參與該項工程的施工時間不得超過20天,則乙隊至少施工多少天才能完成該項工程?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校有一教學樓![]() ,其上有一避雷針
,其上有一避雷針![]() 為
為![]() 米,教學樓后面有一小山,其坡度為
米,教學樓后面有一小山,其坡度為![]() 山坡上有一休息亭
山坡上有一休息亭![]() 供爬山人員休息,測得山坡腳
供爬山人員休息,測得山坡腳![]() 與教學摟的水平距離
與教學摟的水平距離![]() 為
為![]() 米,與休息亭的距離
米,與休息亭的距離![]() 為
為![]() 米,從休息亭
米,從休息亭![]() 測得教學樓上避雷針頂點
測得教學樓上避雷針頂點![]() 的仰角為
的仰角為![]() ,求教學摟
,求教學摟![]() 的高度.(結果保留根號)(注:坡度
的高度.(結果保留根號)(注:坡度![]() 是指坡面的鉛直高度與水平寬度的比)
是指坡面的鉛直高度與水平寬度的比)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,與反比例函數
,與反比例函數![]() 的圖象在第四象限交于點
的圖象在第四象限交于點![]() ,
,![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() ,
,![]() .
.
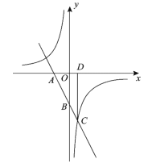
(1)求該反比例函數的表達式;
(2)點![]() 是這個反比例函數圖象上的點,過點
是這個反比例函數圖象上的點,過點![]() 作
作![]() 軸,垂足為點
軸,垂足為點![]() ,連接
,連接![]() 、
、![]() ,如果
,如果![]() ,直接寫出點
,直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com