【題目】在長方形
中，
，
，現將長方形向右平移
，再向下平移
后到長方形
的位置.
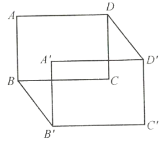
（1）如圖，用
的代數式表示長方形與長方形的重疊部分的面積，這時應滿足怎樣的條件？
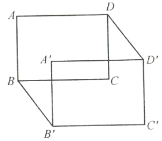
（2）如圖，用的代數式表示六邊形
的面積；
（3）當這兩個長方形沒有重疊部分時，第（2）小題的結論是否改變，請說明理由.
【答案】（1）
，
應滿足的條件是：
；（2）
；（3）不改變，理由詳見解析.
【解析】
（1）表示出重疊部分的長與寬，然后根據長方形的面積公式列式整理即可，根據重疊部分的寬為正數求x的取值范圍；
（2）方法一：利用平移前后的長方形的面積的和加上兩個正方形的面積，然后再減去重疊部分的面積列式進行計算即可得解；
方法二：利用六邊形所在的長方形的面積減去兩個小直角三角形的面積，根據面積公式列式進行計算即可得解．
（3）當這兩個長方形沒有重疊部分時，第（2）小題的結論不改變，延長AD、C′D′交于點M，延長AB、C′B′交于點N，利用S六邊形ABB′C′D′D=S四邊形ANC′M-2S△BNB′求出即可．
解：（1）∵AB=8cm，BC=10cm，
∴重疊部分的長為（10-x），寬為[8-（x+1）]，
∴重疊部分的面積
∵8-（x+1）＞0，
解得x＜7，
∴x應滿足的條件是：0≤x＜7；
（2）方法一：S=10×8×2+
x（x+1）×2-（x2-17x+70），
=160+x2+x-x2+17x-70，
=18x+90（cm2）（0≤x＜7）；
方法二：S=（10+x）（8+x+1）-x（x+1）×2，
=（10+x）（9+x）-x2-x，
=90+19x+x2-x2-x，
=18x+90（cm2）（0≤x＜7）．
（3）當這兩個長方形沒有重疊部分時，第（2）小題的結論不改變．
延長AD、C′D′交于點M，延長AB、C′B′交于點N，
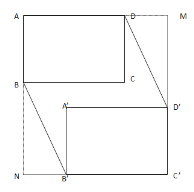
S六邊形ABB′C′D′D=S四邊形ANC′M-2S△BNB′=（10+x）（9+x）-2×x（x+1）=（18x+90）（cm2）．
∴當這兩個長方形沒有重疊部分時，第（2）小題的結論不改變.
科目：初中數學 來源： 題型：
【題目】4月初某地豬肉價格大幅度下調，下調后每千克豬肉的價格是原價格的
，原來用120元買到的豬肉下調后可多買2kg．4月中旬豬肉價格開始回升，經過兩個月后，豬肉價格上調為每千克28.8元．
（1）求4月初豬肉價格下調后變為每千克多少元．
（2）求5、6月份豬肉價格的月平均增長率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】A、B兩輛汽車同時從相距330千米的甲、乙兩地相向而行，s（千米）表示汽車與甲地的距離，t（分）表示汽車行駛的時間，如圖，L1，L2分別表示兩輛汽車的s與t的關系．
（1）L1表示哪輛汽車到甲地的距離與行駛時間的關系？
（2）汽車B的速度是多少？
（3）求L1，L2分別表示的兩輛汽車的s與t的關系式．
（4）2小時后，兩車相距多少千米？
（5）行駛多長時間后，A、B兩車相遇？
查看答案和解析>>
科目：初中數學 來源： 題型：
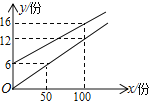
【題目】武漢市某校實行學案式教學，需印制若干份數學學案．印刷廠有甲、乙兩種收費方式，除按印刷份數收取印刷費外，甲種方式還需收取制版費而乙種不需要，兩種印刷方式的費用y（元）與印刷份數x（份）之間的關系如圖所示
(1) 求甲、乙兩種收費方式的函數關系式；
(2) 當印刷多少份學案時，兩種印刷方式收費一樣?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所給圖案，可看作是基本圖形“______”經______次平移得到的，也可看作是基本圖形“______”繞中心旋轉______次得到，還可看作是基本圖形“______”經軸對稱得到整個圖案的.
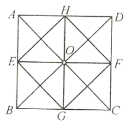
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】新華文具用品店最近購進了一批鋼筆，進價為每支6元，為了合理定價，在銷售前4天試行機動價格，賣出時每支以10元為標準，超過10元的部分記為正，不足10元的部分記為負。文具店記錄了這四天該鋼筆的售價情況和售出情況，如下表所示：
第1天 | 第2天 | 第3天 | 第4天 | |
每支價格相對標準價格(元) | +1 | 0 | -1 | -2 |
售出支數(支) | 12 | 15 | 32 | 33 |
(1)填空：這四天中賺錢最多的是第______天，這天賺了______元錢；
(2)求新華文具用品店這四天出售這種鋼筆一共賺了多少錢；
(3)新華文具用品店準備用這四天賺的錢全部購進這種鋼筆，進價仍為每支6元為了促銷這種鋼筆，每只鋼筆的售價在10元的基礎上打九折，本次購進的這種鋼筆全部售出后共賺了多少錢?
查看答案和解析>>
科目：初中數學 來源： 題型：
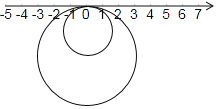
【題目】如圖，半徑為1的小圓與半徑為2的大圓上有一點與數軸上原點重合，兩圓在數軸上做無滑動的滾動，小圓的運動速度為每秒π個單位，大圓的運動速度為每秒2π個單位．
（1）若大圓沿數軸向左滾動1周，則該圓與數軸重合的點所表示的數是 ；
（2）若小圓不動，大圓沿數軸來回滾動，規定大圓向右滾動時間記為正數，向左滾動時間記為負數，依次滾動的情況記錄如下（單位：秒）：﹣1，+2，﹣4，﹣2，+3，﹣8
①第幾次滾動后，大圓離原點最遠？
②當大圓結束運動時，大圓運動的路程共有多少？此時兩圓與數軸重合的點之間的距離是多少？（結果保留π）
（3）若兩圓同時在數軸上各自沿著某一方向連續滾動，滾動一段時間后兩圓與數軸重合的點之間相距9π，求此時兩圓與數軸重合的點所表示的數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形
中，點
、
是正方形內兩點，
，
，為探索這個圖形的特殊性質，某數學興趣小組經歷了如下過程：
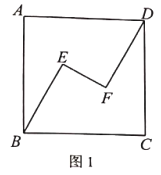
（1）在圖1中，連接
，且
①求證：
與互相平分；
②求證：
；
（2）在圖2中，當
，其它條件不變時，是否成立？若成立，請證明：若不成立，請說明理由.
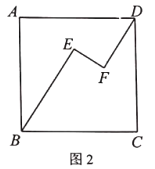
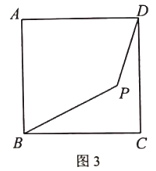
（3）在圖3中，當
，
，
時，求
之長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數y=ax2﹣4ax+3a．
（Ⅰ）求該二次函數的對稱軸；
（Ⅱ）若該二次函數的圖象開口向下，當1≤x≤4時，y的最大值是2，且當1≤x≤4時，函數圖象的最高點為點P，最低點為點Q，求△OPQ的面積；
（Ⅲ）若對于該拋物線上的兩點P（x1，y1），Q（x2，y2），當t≤x1≤t+1，x2≥5時，均滿足y1≥y2，請結合圖象，直接寫出t的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com