
【題目】數和形是數學的兩個主要研究對象,我們經常運用數形結合、數形轉化的方法解決一些數學問題。下面我們來探究“由數思形,以形助數”的方法在解決代數問題中的應用.
探究一:求不等式![]() 的解集
的解集
(1)探究![]() 的幾何意義
的幾何意義
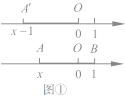
如圖①,在以O為原點的數軸上,設點A'對應點的數為![]() ,由絕對值的定義可知,點A'與O的距離為
,由絕對值的定義可知,點A'與O的距離為![]() ,
,
可記為:A'O=![]() 。將線段A'O向右平移一個單位,得到線段AB,,此時點A對應的數為
。將線段A'O向右平移一個單位,得到線段AB,,此時點A對應的數為![]() ,點B的對應數是1,
,點B的對應數是1,
因為AB= A'O,所以AB=![]() 。
。
因此,![]() 的幾何意義可以理解為數軸上
的幾何意義可以理解為數軸上![]() 所對應的點A與1所對應的點B之間的距離AB。
所對應的點A與1所對應的點B之間的距離AB。
(2)求方程![]() =2的解
=2的解
因為數軸上3與![]() 所對應的點與1所對應的點之間的距離都為2,所以方程的解為
所對應的點與1所對應的點之間的距離都為2,所以方程的解為![]()
(3)求不等式![]() 的解集
的解集
因為![]() 表示數軸上
表示數軸上![]() 所對應的點與1所對應的點之間的距離,所以求不等式解集就轉化為求這個距離小于2的點所對應的數
所對應的點與1所對應的點之間的距離,所以求不等式解集就轉化為求這個距離小于2的點所對應的數![]() 的范圍。
的范圍。
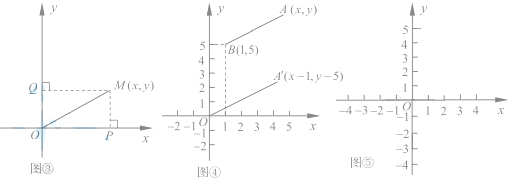
請在圖②的數軸上表示![]() 的解集,并寫出這個解集
的解集,并寫出這個解集
![]()
探究二:探究![]() 的幾何意義
的幾何意義
(1)探究![]() 的幾何意義
的幾何意義
如圖③,在直角坐標系中,設點M的坐標為![]() ,過M作MP⊥x軸于P,作MQ⊥y軸于Q,則點P點坐標(
,過M作MP⊥x軸于P,作MQ⊥y軸于Q,則點P點坐標(![]() ),Q點坐標(
),Q點坐標(![]() ),|OP|=
),|OP|=![]() ,|OQ|=
,|OQ|=![]() ,
,
在Rt△OPM中,PM=OQ=y,則![]()
因此![]() 的幾何意義可以理解為點M
的幾何意義可以理解為點M![]() 與原點O(0,0)之間的距離OM
與原點O(0,0)之間的距離OM
(2)探究![]() 的幾何意義
的幾何意義
如圖④,在直角坐標系中,設點 A'的坐標為![]() ,由探究(二)(1)可知,
,由探究(二)(1)可知,
A'O=![]() ,將線段 A'O先向右平移1個單位,再向上平移5個單位,得到線段AB,此時A的坐標為(
,將線段 A'O先向右平移1個單位,再向上平移5個單位,得到線段AB,此時A的坐標為(![]() ),點B的坐標為(1,5)。
),點B的坐標為(1,5)。
因為AB= A'O,所以 AB=![]() ,因此
,因此![]() 的幾何意義可以理解為點A(
的幾何意義可以理解為點A(![]() )與點B(1,5)之間的距離。
)與點B(1,5)之間的距離。
(3)探究![]() 的幾何意義
的幾何意義
請仿照探究二(2)的方法,在圖⑤中畫出圖形,并寫出探究過程。
(4)![]() 的幾何意義可以理解為:_________________________.
的幾何意義可以理解為:_________________________.
拓展應用:
(1)![]() +
+![]() 的幾何意義可以理解為:點A
的幾何意義可以理解為:點A![]() 與點E
與點E![]() 的距離與點AA
的距離與點AA![]() 與點F____________(填寫坐標)的距離之和。
與點F____________(填寫坐標)的距離之和。
(2)![]() +
+![]() 的最小值為____________(直接寫出結果)
的最小值為____________(直接寫出結果)
【答案】探究一(3)  解集為:
解集為:![]()
探究二(3)(![]() )拓展應用(1)(
)拓展應用(1)(![]() ) (2)5
) (2)5
【解析】
試題分析:探究一(3):![]() 的解集就是數軸上
的解集就是數軸上![]() 所對應的點與1所對應的點之間的距離小于2的點所對應的數,利用數軸可知
所對應的點與1所對應的點之間的距離小于2的點所對應的數,利用數軸可知![]()
探究二(3):根據題目信息,![]() 的幾何意義可以理解為點A(
的幾何意義可以理解為點A(![]() )與點B(
)與點B(![]() )之間的距離。
)之間的距離。
拓展應用:根據題目信息知是與點F(![]() )的距離之和。
)的距離之和。
![]() +
+![]() 表示點A
表示點A![]() 與點E
與點E![]() 的距離與點A
的距離與點A![]() 與點F(
與點F(![]() )的距離之和。∴最小值為E
)的距離之和。∴最小值為E![]() 與點F(
與點F(![]() )的距離5.
)的距離5.
試題解析:探究一
(3) 
解集為:![]()
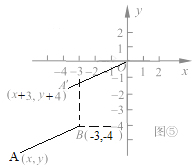
探究二(3)
如圖⑤,在直角坐標系中,設點 A'的坐標為![]() ,
,
由探究(二)(1)可知, A'O=![]() ,
,
將線段 A'O先向左平移3個單位,再向下平移4個單位,
得到線段AB,此時A的坐標為(![]() ),點B的坐標為(
),點B的坐標為(![]() )。
)。
因為AB= A'O,所以 AB=![]() ,
,
因此![]() 的幾何意義可以理解為點A(
的幾何意義可以理解為點A(![]() )與點B(
)與點B(![]() )之間的距離。
)之間的距離。
拓展應用
(1)(![]() ) (2)5
) (2)5


科目:初中數學 來源: 題型:
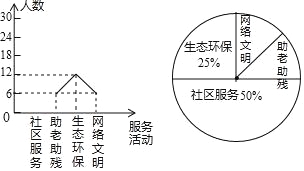
【題目】為大力弘揚“奉獻、友愛、互助、進步”的志愿服務精神,傳播“奉獻他人、提升自我”的志愿服務理念,東營市某中學利用周末時間開展了“助老助殘、社區服務、生態環保、網絡文明”四個志愿服務活動(每人只參加一個活動),九年級某班全班同學都參加了志愿服務,班長為了解志愿服務的情況,收集整理數據后,繪制以下不完整的統計圖,請你根據統計圖中所提供的信息解答下列問題:
(1)求該班的人數;
(2)請把折線統計圖補充完整;
(3)求扇形統計圖中,網絡文明部分對應的圓心角的度數;
(4)小明和小麗參加了志愿服務活動,請用樹狀圖或列表法求出他們參加同一服務活動的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校學生對《最強大腦》、《朗讀者》、《中國詩詞大會》、《出彩中國人》四個電視節目的喜愛情況,隨機抽取了![]() 名學生進行調查統計(要求每名學生選出并且只能選出一個自己最喜愛的節目),并將調查結果繪制成如下統計圖表:
名學生進行調查統計(要求每名學生選出并且只能選出一個自己最喜愛的節目),并將調查結果繪制成如下統計圖表:
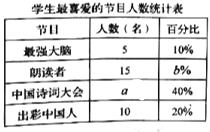

根據以上提供的信息,解答下列問題:
(1)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)補全上面的條形統計圖;
(3)若該校共有學生1000名.根據抽樣調查結果,估計該校最喜愛《中國詩詞大會》節目的學生有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC.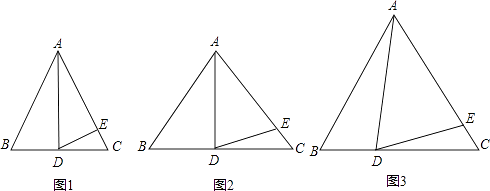
(1)如圖1,如果∠BAD=30°,AD是BC上的高,AD=AE,則∠EDC=
(2)如圖2,如果∠BAD=40°,AD是BC上的高,AD=AE,則∠EDC=
(3)思考:通過以上兩題,你發現∠BAD與∠EDC之間有什么關系?請用式子表示:
(4)如圖3,如果AD不是BC上的高,AD=AE,是否仍有上述關系?如有,請你寫出來,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com