
【題目】已知:![]() 中,
中,![]() 是直徑,弦
是直徑,弦![]() .
.
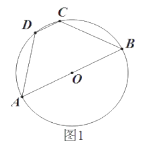
![]() 如圖1,求證:
如圖1,求證:![]()
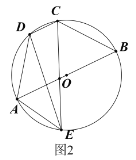
![]() 如圖2,點(diǎn)
如圖2,點(diǎn)![]() 在圓上,連接
在圓上,連接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
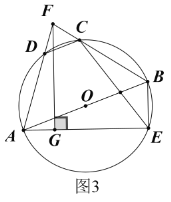
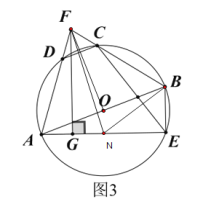
![]() 如圖3,在
如圖3,在![]() 的條件下,分別延長線段
的條件下,分別延長線段![]() 交于點(diǎn)
交于點(diǎn)![]() ,過
,過![]() 作
作![]() 于
于![]() ,連接
,連接![]() ,若
,若![]() ,求
,求![]() 的長.
的長.
【答案】![]() 詳見解析;
詳見解析; ![]() ;
; ![]()
【解析】
(1)連接OC,OD,證明△AOD≌△BOC即可;
(2)作直徑DQ,連接CQ,則∠DCQ=90°,根據(jù)DC∥AB,可得∠CHB=∠DCQ=90°,根據(jù)弧DC=弧DC,可得tan∠Q=tan∠DEC=![]() ,可設(shè)DC=7k,則CQ=24k,根據(jù)已知可得出CH=
,可設(shè)DC=7k,則CQ=24k,根據(jù)已知可得出CH=![]() CQ=12k,HB=9k,即可得出tan∠B,根據(jù)弧AC=弧AC,可得∠CEA=∠B,即可得出答案;
CQ=12k,HB=9k,即可得出tan∠B,根據(jù)弧AC=弧AC,可得∠CEA=∠B,即可得出答案;
(3)由現(xiàn)有條件可得AF=BF,連接FO,得∠OFG=∠EAB=α,再設(shè)∠AFG=β,在AE上取GN=AG=3,連接FN,則FN=FA=FB,推出tan∠NBE=![]() ,設(shè)BE=3n,則NE=4n,GE=2BE=6n,可推出AB=
,設(shè)BE=3n,則NE=4n,GE=2BE=6n,可推出AB=![]() =
=![]() ,所以在Rt△FOB中,tan∠OBF=
,所以在Rt△FOB中,tan∠OBF=![]() ,設(shè)FO=4t,OB=3t,即可得出FB,根據(jù)FA=FB即可確定答案.
,設(shè)FO=4t,OB=3t,即可得出FB,根據(jù)FA=FB即可確定答案.
(1)如圖,連接OC,OD,

∵OC=OD,
∴∠ODC=∠OCD,
∵DC∥AB,
∴∠AOD=∠ODC=∠OCD=∠BOC,
又∵OA=OB,
∴△AOD≌△BOC,
∴AD=BC;
(2)作直徑DQ,連接CQ,則∠DCQ=90°,
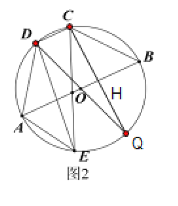
∵DC∥AB,
∴∠CHB=∠DCQ=90°,
又∵AB是直徑,
∴CH=QH=![]() CQ,
CQ,
∴OH是△DCQ的中位線,
∴OH=![]() DC,
DC,
∵弧DC=弧DC,
∴∠DEC=∠Q,
∴tan∠Q=tan∠DEC=![]() ,
,
設(shè)DC=7k,則CQ=24k,
∴CH=![]() CQ=12k,OH=
CQ=12k,OH=![]() DC=
DC=![]() k,
k,
2r=DQ=![]() =25k,
=25k,
∴OB=r=![]() k,
k,
∴HB=OB-OH=![]() k-
k-![]() k=9k,
k=9k,
∴tan∠B=![]() =
=![]() =
=![]() ,
,
∵弧AC=弧AC,
∴∠CEA=∠B,
∴tan∠CEA= tan∠B=![]() ;
;
(3)如圖1,
∵∠AOD =∠BOC,
∴∠AOD+∠DOC=∠BOC+∠DOC,即∠AOC=∠BOD,
∴弧AC=弧BD,
∴∠FAB=∠FBA,
∴AF=BF,
如圖3,連接FO,
∵AO=BO,
∴∠BFO=∠AFO,FO⊥AB,
又∵FG⊥AE,
∴∠FOA=∠AGF=90°,
∴∠OFG=∠EAB=α,
設(shè)∠AFG=β,
則∠BFO=∠AFO=∠OFG+∠AFG=α+β,
∴∠AFB=2(α+β),
在AE上取GN=AG=3,連接FN,則FN=FA=FB,
∴∠GFN=∠AFG=β,
∴∠NFB=∠AFB-∠AFN=2(α+β)-2β=2α,
∴∠FBN=∠FNB=![]() =90°-α,
=90°-α,
∵AB是直徑,
∴∠AEB=90°,
∴∠ABE=90°-∠EAB=90°-α=∠FBN,
∴∠ABE-∠ABN=∠FBN-∠ABN,
∴∠NBE=∠ABC,
∴tan∠NBE=![]() ,
,
∴設(shè)BE=3n,則NE=4n,
GE=2BE=6n,
∴6n=3+4n,
∴n=![]() ,
,
∴BE=![]() ,AE=12,
,AE=12,
∴AB=![]() =
=![]() ,
,
在Rt△FOB中,tan∠OBF=![]() ,
,
∴設(shè)FO=4t,OB=3t,
∴FB=![]() =5t,
=5t,
∴FB=![]() OB=
OB=![]() ×
×![]() =
=![]() ,
,
∴FA=FB=![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如下表,從左邊第一個格子開始向右數(shù),在每個小格子中都填入一個整數(shù),使得其中仼意三個相鄰格子中所填整數(shù)之和都相等.
|
|
|
| 5 | 4 | …… |
(1)可求得![]() _____;
_____;![]() _____;
_____;![]() _____.
_____.
(2)第2019個格子中的數(shù)為______;
(3)前2020個格子中所填整數(shù)之和為______.
(4)前![]() 個格子中所填整數(shù)之和是否可能為2020?若能,求出
個格子中所填整數(shù)之和是否可能為2020?若能,求出![]() 的值,若不能,請說明理由.
的值,若不能,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
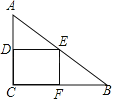
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的頂點(diǎn)E在邊AB上,D,F兩點(diǎn)分別在邊AC,BC上,且![]() ,將矩形CDEF以每秒1個單位長度的速度沿射線CB方向勻速運(yùn)動,當(dāng)點(diǎn)C與點(diǎn)B重合時停止運(yùn)動,設(shè)運(yùn)動時間為t秒,矩形CDEF與△ABC重疊部分的面積為S,則反映S與t的函數(shù)關(guān)系的圖象為( )
,將矩形CDEF以每秒1個單位長度的速度沿射線CB方向勻速運(yùn)動,當(dāng)點(diǎn)C與點(diǎn)B重合時停止運(yùn)動,設(shè)運(yùn)動時間為t秒,矩形CDEF與△ABC重疊部分的面積為S,則反映S與t的函數(shù)關(guān)系的圖象為( )
A.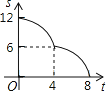 B.
B.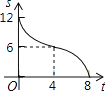 C.
C. D.
D.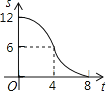
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
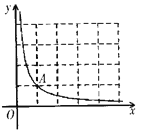
【題目】如圖,在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,直線
,直線![]() 與曲線
與曲線![]() 圍成的封閉區(qū)域?yàn)閳D象
圍成的封閉區(qū)域?yàn)閳D象![]() .
.
(1)求曲線![]() 的表達(dá)式;
的表達(dá)式;
(2)求出直線與曲線的交點(diǎn)坐標(biāo);
(3)直接寫出圖象![]() 上的整數(shù)點(diǎn)個數(shù)有_________個,它們是___________.
上的整數(shù)點(diǎn)個數(shù)有_________個,它們是___________.
(注:橫,縱坐標(biāo)均為整數(shù)的點(diǎn)稱為整點(diǎn),圖象![]() 包含邊界)
包含邊界)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 圖象的頂點(diǎn)坐標(biāo)為(3,8),該二次函數(shù)圖像的對稱軸與
圖象的頂點(diǎn)坐標(biāo)為(3,8),該二次函數(shù)圖像的對稱軸與![]() 軸的交點(diǎn)為A,M是這個二次函數(shù)圖像上的點(diǎn),
軸的交點(diǎn)為A,M是這個二次函數(shù)圖像上的點(diǎn),![]() 是原點(diǎn)
是原點(diǎn)
(1)不等式![]() 是否成立?請說明理由;
是否成立?請說明理由;
(2)設(shè)![]() 是△AMO的面積,求滿足
是△AMO的面積,求滿足![]() 的所有點(diǎn)M的坐標(biāo).
的所有點(diǎn)M的坐標(biāo).
(3)將(2)中符號條件的點(diǎn)M聯(lián)結(jié)起來構(gòu)成怎樣的特殊圖形?寫出兩條這個特殊圖形的性質(zhì).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
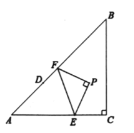
【題目】如圖,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 分別在邊
分別在邊![]() 上,
上,![]() ,點(diǎn)
,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 向點(diǎn)
向點(diǎn)![]() 運(yùn)動,運(yùn)動到點(diǎn)
運(yùn)動,運(yùn)動到點(diǎn)![]() 結(jié)束,以
結(jié)束,以![]() 為斜邊作等腰直角三角形
為斜邊作等腰直角三角形 ![]() (點(diǎn)
(點(diǎn)![]() 按順時針排列) ,在點(diǎn)
按順時針排列) ,在點(diǎn)![]() 運(yùn)動過程中點(diǎn)
運(yùn)動過程中點(diǎn)![]() 經(jīng)過的路徑長是 __________
經(jīng)過的路徑長是 __________
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
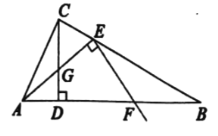
【題目】如圖,已知![]() 是
是![]() 的高,
的高, ![]() 直角
直角![]() 的頂點(diǎn)
的頂點(diǎn)![]() 是射線
是射線![]() 上一動點(diǎn),
上一動點(diǎn), ![]() 交直線
交直線![]() 于點(diǎn)
于點(diǎn)![]() 所在直線交直線
所在直線交直線![]() 于點(diǎn)F.
于點(diǎn)F.
(1)判斷△ABC的形狀,并說明理由;
(2)若G為AE的中點(diǎn),求tan∠EAF的值;
(3)在點(diǎn)E的運(yùn)動過程中,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,與x軸交于兩點(diǎn)A,B(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C.
,與x軸交于兩點(diǎn)A,B(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C.
(Ⅰ)求點(diǎn)A,B和點(diǎn)C的坐標(biāo);
(Ⅱ)已知P是線段![]() 上的一個動點(diǎn).
上的一個動點(diǎn).
①若![]() 軸,交拋物線于點(diǎn)Q,當(dāng)
軸,交拋物線于點(diǎn)Q,當(dāng)![]() 取最大值時,求點(diǎn)P的坐標(biāo);
取最大值時,求點(diǎn)P的坐標(biāo);
②求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,E是BC的中點(diǎn),以AC為直徑的⊙O與AB邊交于點(diǎn)D,連接DE.
(1)求證:DE是⊙O的切線;
(2)若CD=6cm,DE=5cm,求⊙O直徑的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com