
【題目】已知方程![]() ,
,
(1)求證:方程一定有兩個(gè)不相等的實(shí)數(shù)根;
(2)![]() 取何值時(shí),方程二根中一個(gè)比3大,一個(gè)比3小。(可用數(shù)形結(jié)合來(lái)解)
取何值時(shí),方程二根中一個(gè)比3大,一個(gè)比3小。(可用數(shù)形結(jié)合來(lái)解)
(3)![]() 取何值時(shí)方程的兩個(gè)根異號(hào)且負(fù)的實(shí)數(shù)根的絕對(duì)值大.
取何值時(shí)方程的兩個(gè)根異號(hào)且負(fù)的實(shí)數(shù)根的絕對(duì)值大.
【答案】(1)見解析;(2)a>1;(3)a<0.
【解析】
(1)求出△的值,再判斷即可;
(2)由題意得![]() ,即
,即![]() ,再根據(jù)根與系數(shù)關(guān)系解答即可;
,再根據(jù)根與系數(shù)關(guān)系解答即可;
(3)由題意可得x1+x2<0,x1x2<0,,根據(jù)根與系數(shù)關(guān)系即可解答.
解:(1)方程x2-2ax+a=4,可化為:x2-2ax+a-4=0,
∴△=4a2-4(a-4)=4(a![]() )2+15>0,故方程一定有兩個(gè)不相等的實(shí)數(shù)根;
)2+15>0,故方程一定有兩個(gè)不相等的實(shí)數(shù)根;
(2)∵方程二根中一個(gè)比3大,一個(gè)比3小,
∴![]()
![]()
∵x1+x2=2a,x1x2=a-4,
∴(a-4)-3×2a +9<0,
解得:a>1,
∴a>1時(shí),方程二根中一個(gè)比3大,一個(gè)比3小;
(3)若方程有兩根相異,并且負(fù)根的絕對(duì)值較大,則可得:x1+x2=2a<0,x1x2=a-4<0,解得:a<0.
故答案為:(1)見解析;(2)a>1;(3)a<0.


 活力課時(shí)同步練習(xí)冊(cè)系列答案
活力課時(shí)同步練習(xí)冊(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
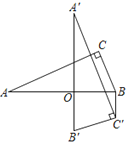
【題目】如圖,在Rt△ABC中,∠C=90°,AC=12,BC=5,將△ABC繞AB上的點(diǎn)O順時(shí)針旋轉(zhuǎn)90°,得到△A'B'C',連結(jié)BC'.若BC'∥A'B',則OB的值為( )
A. ![]() B. 5C.
B. 5C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為發(fā)展校園足球運(yùn)動(dòng),某縣城區(qū)四校決定聯(lián)合購(gòu)買一批足球運(yùn)動(dòng)裝備,市場(chǎng)調(diào)查發(fā)現(xiàn):甲、乙兩商場(chǎng)以同樣的價(jià)格出售同種品牌的足球隊(duì)服和足球,已知每套隊(duì)服比每個(gè)足球多50元,兩套隊(duì)服與三個(gè)足球的費(fèi)用相等,經(jīng)洽談,甲商場(chǎng)優(yōu)惠方案是:每購(gòu)買十套隊(duì)服,送一個(gè)足球;乙商場(chǎng)優(yōu)惠方案是:若購(gòu)買隊(duì)服超過(guò)80套,則購(gòu)買足球打八折.
(1)求每套隊(duì)服和每個(gè)足球的價(jià)格是多少?
(2)若城區(qū)四校聯(lián)合購(gòu)買100套隊(duì)服和a個(gè)足球,請(qǐng)用含a的式子分別表示出到甲商場(chǎng)和乙商場(chǎng)購(gòu)買裝備所花的費(fèi)用;
(3)假如你是本次購(gòu)買任務(wù)的負(fù)責(zé)人,你認(rèn)為到哪家商場(chǎng)購(gòu)買比較合算?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
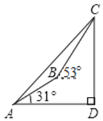
【題目】鄂州市電信部門積極支持鄂州國(guó)際航空大都市的建設(shè),如圖,計(jì)劃修建一條連接B,C兩地的電纜,測(cè)量人員在山腳A測(cè)得B,C兩地的仰角分別為31°和45°,在B處測(cè)得C處的仰角為53°.已知C地比A地髙50m,則電纜BC至少需要多少米?(精確到1m,參考數(shù)據(jù):sin31°≈![]() ,tan31°≈
,tan31°≈![]() ,sin37°≈0.6,cos37°≈0.8)
,sin37°≈0.6,cos37°≈0.8)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB為⊙O的直徑,射線AP交⊙O于C點(diǎn),∠PCO的平分線交⊙O于D點(diǎn),過(guò)點(diǎn)D作![]() 交AP于E點(diǎn).
交AP于E點(diǎn).
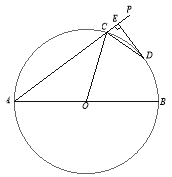
(1)求證:DE為⊙O的切線;
(2)若DE=3,AC=8,求直徑AB的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知頂點(diǎn)為(﹣3,﹣6)的拋物線y=ax2+bx+c經(jīng)過(guò)點(diǎn)(﹣1,﹣4),則下列結(jié)論
①6a﹣b=0;
②abc>0;
③若點(diǎn)M(﹣2,m)與點(diǎn)N(﹣5,n)為拋物線上兩點(diǎn),則m>n;
④ax2+bx+c≥﹣6;
⑤關(guān)于x的一元二次方程ax2+bx+c=﹣4的兩根為﹣5和﹣1.其中正確結(jié)論有( )
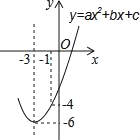
A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有長(zhǎng)為24m的籬笆,現(xiàn)一面利用墻(墻的最大可用長(zhǎng)度a為10m)圍成中間隔有一道籬笆的長(zhǎng)方形花圃,設(shè)花圃的寬AB為xm,面積為Sm2.
(1)求S與x的函數(shù)關(guān)系式及x值的取值范圍;
(2)要圍成面積為45m2的花圃,AB的長(zhǎng)是多少米?
(3)當(dāng)AB的長(zhǎng)是多少米時(shí),圍成的花圃的面積最大?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC中,AB=AC,以AB為直徑的⊙O與BC相交于點(diǎn)D,與CA的延長(zhǎng)線相交于點(diǎn)E,過(guò)點(diǎn)D作DF⊥AC于點(diǎn)F.

(1)試說(shuō)明DF是⊙O的切線;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
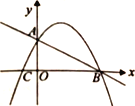
【題目】如圖,直線![]() 交坐標(biāo)軸于A、B兩點(diǎn),直線AC⊥AB交x軸于點(diǎn)C,拋物線恰好過(guò)點(diǎn)A、B、C.
交坐標(biāo)軸于A、B兩點(diǎn),直線AC⊥AB交x軸于點(diǎn)C,拋物線恰好過(guò)點(diǎn)A、B、C.
(1)求拋物線的表達(dá)式.
(2)當(dāng)點(diǎn)M在線段AB上方的曲線上移動(dòng)時(shí),求四邊形AOBM的面積的最大值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com