
【題目】某數學興趣小組在本校九年級學生中以“你最喜歡的項體育運動"為主體進行了抽樣調查,并將調查結果繪制成下表和下圖.
項目 | 籃球 | 乒乓球 | 羽毛球 | 跳繩 | 其他 |
人數 |
| 12 | 10 | 5 | 8 |

請根據圖表中的信息完成下列各題:
(1)本次共調查學生______名;
(2)![]() =______;
=______;
(3)在扇形圖中,“跳繩”對應的扇形圓是______.
【答案】50 15 ![]()
【解析】
(1)設本次共調查了x名學生,由統計表中的數據可知喜歡羽毛球的有10人,由扇形統計圖可知,喜歡羽毛球的人數是總人數的20%,故可得出x的值;
(2)由于喜歡籃球的人數占調查人數的30%,再由(1)中求出的x的值進行計算即可;
(3)由于喜歡跳繩的人數是5人,故可求出所占調查人數的百分比,故可求出對應的扇形圓心角的度數;
解:(1)設本次共調查了x名學生,
∵由統計表中的數據可知喜歡羽毛球的有10人,由扇形統計圖可知,喜歡羽毛球的人數是總人數的20%,
∴![]() ,
,
解得:x=50(人);
∴本次共調查學生50名;
故答案為:50;
(2)∵喜歡籃球的人數占調查人數的30%,共有50人參加調查,
∴a=50×30%=15(人);
故答案為:15;
(3)∵由于喜歡跳繩的人數是5人,
∴![]() ,
,
∴“跳繩”對應的扇形圓心角的度數=![]() ;
;
故答案為:36°.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某商店購進![]() ,
,![]() 兩種商品,購買
兩種商品,購買![]() 個
個![]() 商品比購買
商品比購買![]() 個
個![]() 商品多花
商品多花![]() 元,并且花費
元,并且花費![]() 元購買
元購買![]() 商品和花費
商品和花費![]() 元購買
元購買![]() 商品的數量相等.
商品的數量相等.
(1)求購買一個![]() 商品和一個
商品和一個![]() 商品各需要多少元?
商品各需要多少元?
(2)若商店準備購買![]() ,
,![]() 兩種商品共
兩種商品共![]() 個,并且購買
個,并且購買![]() ,
,![]() 兩種商品的總費用不超過
兩種商品的總費用不超過![]() 元,那么商店至多購買
元,那么商店至多購買![]() 商品多少件?
商品多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系xOy中,一次函數y=﹣![]() x+5的圖象l1分別與x,y軸交于A,B兩點,正比例函數的圖象l2與l1交于點C(m,4).
x+5的圖象l1分別與x,y軸交于A,B兩點,正比例函數的圖象l2與l1交于點C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函數y=kx+1的圖象為l3,且11,l2,l3不能圍成三角形,直接寫出k的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
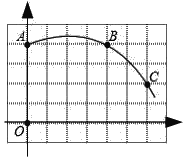
【題目】如圖,網格紙中每個小正方形的邊長為1,一段圓弧經過格點,點O為坐標原點.
(1)該圖中弧所在圓的圓心D的坐標為 ;.
(2)根據(1)中的條件填空:
①圓D的半徑= (結果保留根號);
②點(7,0)在圓D (填“上”、“內”或“外”);
③∠ADC的度數為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰![]() 中,
中,![]() .點
.點![]() 從點
從點![]() 出發沿射線
出發沿射線![]() 方向運動,同時點
方向運動,同時點![]() 從
從![]() 出發,以相同的速度沿射線
出發,以相同的速度沿射線![]() 方向運動,連
方向運動,連![]() ,交直線
,交直線![]() 于點
于點![]()
![]() 當點
當點![]() 運動到
運動到![]() 中點時,求
中點時,求![]() 的長.
的長.
![]() 求證:
求證:![]() .
.
![]() 過點
過點![]() 作
作![]() ,交直線
,交直線![]() 于
于![]() ,請探究
,請探究![]() 之間的數量關系,并直接寫出結論.
之間的數量關系,并直接寫出結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市甲、乙兩個汽車銷售公司,去年一至十月份每月銷售同種品牌汽車的情況如圖所示:
![]() 請你根據上圖填寫下表:
請你根據上圖填寫下表:
銷售公司 | 平均數 | 方差 | 中位數 | 眾數 |
甲 |
| 9 | ||
乙 | 9 |
| 8 |
![]() 請你從以下兩個不同的方面對甲、乙兩個汽車銷售公司去年一至十月份的銷售情況進行分析:
請你從以下兩個不同的方面對甲、乙兩個汽車銷售公司去年一至十月份的銷售情況進行分析:
![]() 從平均數和方差結合看;
從平均數和方差結合看;
![]() 從折線圖上甲、乙兩個汽車銷售公司銷售數量的趨勢看
從折線圖上甲、乙兩個汽車銷售公司銷售數量的趨勢看![]() 分析哪個汽車銷售公司較有潛力
分析哪個汽車銷售公司較有潛力![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,網格紙中每個小正方形的邊長為1,一段圓弧經過格點,點O為坐標原點.
(1)該圖中弧所在圓的圓心D的坐標為 ;.
(2)根據(1)中的條件填空:
①圓D的半徑= (結果保留根號);
②點(7,0)在圓D (填“上”、“內”或“外”);
③∠ADC的度數為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
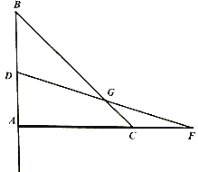
【題目】如圖1,直線![]() 分別與
分別與![]() 軸交于
軸交于![]() 兩點,過點
兩點,過點![]() 的直線交
的直線交![]() 軸負半軸于
軸負半軸于![]() ,且
,且![]() .
.

(1)求直線![]() 的函數表達式:
的函數表達式:
(2)如圖2, ![]() 為
為![]() 軸上
軸上![]() 點右側的一動點,以
點右側的一動點,以![]() 為直角頂點,
為直角頂點,![]() 為一腰在第一象限內作等腰直角三角形
為一腰在第一象限內作等腰直角三角形![]() ,連接
,連接![]() 并延長交
并延長交![]() 軸于點
軸于點![]() .當
.當![]() 點運動時,
點運動時,![]() 點的位置是否發生變化?如果不變請求出它的坐標:如果變化,請說明理由.
點的位置是否發生變化?如果不變請求出它的坐標:如果變化,請說明理由.
(3)直線![]() 交
交![]() 于
于![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 軸于
軸于![]() ,是否存在這樣的直線
,是否存在這樣的直線![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
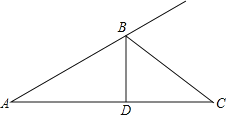
【題目】如圖,在△ABC中,BD⊥AC,垂足為C,且∠A<∠C,點E是一動點,其在BC上移動,連接DE,并過點E作EF⊥DE,點F在AB的延長線上,連接DF交BC于點G.
(1)請同學們根據以上提示,在上圖基礎上補全示意圖.
(2)當△ABD與△FDE全等,且AD=FE,∠A=30°,∠AFD=40°,求∠C的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com