
【題目】在學習軸對稱的時候,老師讓同學們思考課本中的探究題.
如圖(1),要在燃氣管道l上修建一個泵站,分別向A、B兩鎮供氣.泵站修在管道的什么地方,可使所用的輸氣管線最短?
你可以在l上找幾個點試一試,能發現什么規律?你可以在![]() 上找幾個點試一試,能發現什么規律?
上找幾個點試一試,能發現什么規律?
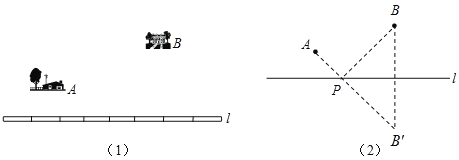
聰明的小華通過獨立思考,很快得出了解決這個問題的正確辦法.他把管道l看成一條直線(圖(2)),問題就轉化為,要在直線l上找一點P,使AP與BP的和最小.他的做法是這樣的:
①作點B關于直線l的對稱點B′.
②連接AB′交直線l于點P,則點P為所求.
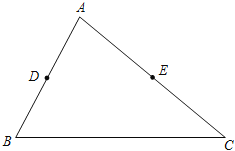
請你參考小華的做法解決下列問題.如圖在△ABC中,點D、E分別是AB、AC邊的中點,BC=6,BC邊上的高為4,請你在BC邊上確定一點P,使△PDE得周長最小.
(1)在圖中作出點P(保留作圖痕跡,不寫作法).
(2)請直接寫出△PDE周長的最小值:
.
科目:初中數學 來源: 題型:
【題目】如圖,由一段斜坡AB的高AD長為0.6米,∠ABD=30°,為了達到無障礙通道的坡道標準,現準備把斜坡改長,使∠ACD=5.71°.
(1)求斜坡AB的長;
(2)求斜坡新起點C與原起點B的距離.(精確到0.01米)(參考數據:![]() ≈1.732,tan5.71°≈0.100)
≈1.732,tan5.71°≈0.100)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司銷售A,B兩種品牌的教學設備,這兩種教學設備的進價和售價如表所示
A | B | |
進價(萬元/套) | 1.5 | 1.2 |
售價(萬元/套) | 1.8 | 1.4 |
該公司計劃購進兩種教學設備若干套,共需66萬元,全部銷售后可獲毛利潤12萬元.
(1)該公司計劃購進A,B兩種品牌的教學設備各多少套?
(2)通過市場調研,該公司決定在原計劃的基礎上,減少A種設備的購進數量,增加B種設備的購進數量,已知B種設備增加的數量是A種設備減少的數量的1.5倍.若用于購進這兩種教學設備的總資金不超過68萬元,問A種設備購進數量至多減少多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校準備成立男女校足球隊,為了解全校學生對足球的喜愛程度,該校設計了一個調查問卷,將喜愛程度分為A(非常喜歡)、B(喜歡)、C(不太喜歡),D(很不喜歡)四種類型,并派學生會會員進行市場調查,其中一名學生會會員小麗在校門口對上學學生進行了隨機調查,并根據調查結果制成了如下兩幅不完整的統計圖,請結合統計圖所給信息解答下列問題:
(1)在扇形統計圖(圖1)中C所占的百分比是 ;小麗本次抽樣調查的人數共有 人;
請將折線統計圖(圖2)補充完整;
(2)為了解少數學生很不喜歡足球的原因,小麗決定在上述調查結果中從“很不喜歡”足球的學生里隨機選
出兩位進行回訪,請你用列表法或畫樹狀圖的方法,求所選出的兩位學生恰好是一男一女的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
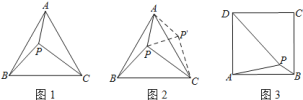
小偉遇到這樣一個問題:如圖![]() ,在正三角形
,在正三角形![]() 內有一點
內有一點![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數.小偉是這樣思考的:如圖
的度數.小偉是這樣思考的:如圖![]() ,利用旋轉和全等的知識構造
,利用旋轉和全等的知識構造![]() ,連接
,連接![]() ,得到兩個特殊的三角形,從而將問題解決.
,得到兩個特殊的三角形,從而將問題解決.
(1)請你回答:圖![]() 中
中![]() 的度數等于________.
的度數等于________.
參考小偉同學思考問題的方法,解決下列問題:
(2)如圖![]() ,在正方形
,在正方形![]() 內有一點
內有一點![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數和正方形的邊長.
的度數和正方形的邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在梯形![]() 中,
中,![]() ,中位線
,中位線![]() 與對角線
與對角線![]() 交于
交于![]() 兩點,若
兩點,若![]() cm,
cm, ![]() cm,則
cm,則![]() 的長等于( )
的長等于( )

A. 10 cm B. 13 cm C. 20 cm D. 26 cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 如圖一:小明想測量一棵樹的高度
如圖一:小明想測量一棵樹的高度![]() ,在陽光下,小明測得一根與地面垂直、長為
,在陽光下,小明測得一根與地面垂直、長為![]() 米的竹竿的影長為
米的竹竿的影長為![]() 米.同時另一名同學測量一棵樹的高度時,發現樹的影子不全落在地面上,有一部分影子落在教學樓的墻壁上(如圖),墻壁上的影長
米.同時另一名同學測量一棵樹的高度時,發現樹的影子不全落在地面上,有一部分影子落在教學樓的墻壁上(如圖),墻壁上的影長![]() 為
為![]() 米,落在地面上的影長
米,落在地面上的影長![]() 為
為![]() 米,則樹高
米,則樹高![]() 為多少米.
為多少米.
![]() 如圖二:在陽光下,小明在某一時刻測得與地面垂直、長為
如圖二:在陽光下,小明在某一時刻測得與地面垂直、長為![]() 的桿子在地面上的影子長為
的桿子在地面上的影子長為![]() ,在斜坡上影長為
,在斜坡上影長為![]() ,他想測量電線桿
,他想測量電線桿![]() 的高度,但其影子恰好落在土坡的坡面
的高度,但其影子恰好落在土坡的坡面![]() 和地面
和地面![]() 上,量得
上,量得![]() ,
,![]() ,求電線桿的高度.
,求電線桿的高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】運算能力是一項重要的數學能力.王老師為幫助學生診斷和改進運算中的問題,對全班學生進行了三次運算測試.下面的氣泡圖中,描述了其中5位同學的測試成績.(氣泡圓的圓心橫、縱坐標分別表示第一次和第二次測試成績,氣泡的大小表示三次成績的平均分的高低;氣泡越大平均分越高.)

①在5位同學中,有_____位同學第一次成績比第二次成績高;
②在甲、乙兩位同學中,第三次成績高的是_____.(填“甲”或“乙”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,分別以Rt△ABC的直角邊AC、BC為邊,在Rt△ABC外作兩個等邊三角形△ACE和△BCF,連接BE、AF分別交AC、BC邊于H、D兩點.下列結論:①AF=BE;②∠AFC=∠EBC;③∠FAE=90°;④BD=FD,其中正確結論的個數是( )

A.4個B.3個C.2個D.1個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com