
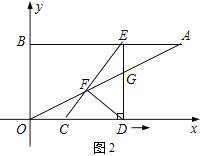
【題目】如圖1,已知點A(8,4),點B(0,4),線段CD的長為3,點C與原點O重合,點D在x軸正半軸上.線段CD沿x軸正方向以每秒1個單位長度的速度向右平移,過點D作x軸的垂線交線段AB于點E,交OA于點G,連接CE交OA于點F(如圖2),設運動時間為t.當E點與A點重合時停止運動.
(1)求線段CE的長;
(2)記△CDE與△ABO公共部分的面積為S,求S關于t的函數關系式;
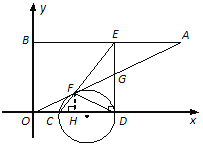
(3)如圖2,連接DF.
①當t取何值時,以C、F、D為頂點的三角形為等腰三角形?
②△CDF的外接圓能否與OA相切?如果能,直接寫出此時t的值;如果不能,請說明理由.

【答案】(1)5;(2)S=![]() (5-t )2(0≤t≤5);(3)①t=3或
(5-t )2(0≤t≤5);(3)①t=3或![]() 或
或 ![]() 時,△CDF為等腰三角形;②能 t=
時,△CDF為等腰三角形;②能 t=![]() .
.
【解析】分析:(1)、根據Rt△CDE的勾股定理求出CE的長度;(2)、作FH⊥CD于H,根據題意得出△OCF∽△AEF和△ODG∽△AEG,得出![]() 和
和![]() 的采購員CF和EG的長度,然后根據FH∥ED得出
的采購員CF和EG的長度,然后根據FH∥ED得出 ![]() ,從而求出HD的長度,最后根據S=
,從而求出HD的長度,最后根據S= ![]() EG·HD得出函數解析式;(3)、根據CF=CD、CF=DF和DF=CD三種情況分別求出t的值;作FH⊥CD于H得出△FCH∽△ECD,從而得出
EG·HD得出函數解析式;(3)、根據CF=CD、CF=DF和DF=CD三種情況分別求出t的值;作FH⊥CD于H得出△FCH∽△ECD,從而得出![]() ,然后求出
,然后求出![]() ,
,![]() ,
,![]() ,根據切割線定理得出OF2=OC
,根據切割線定理得出OF2=OC![]() OD,從而得出t的值.
OD,從而得出t的值.
詳解:(1)在Rt△CDE中,CD=3,DE=4, ∴CE=![]() =5,
=5,

(2)作FH⊥CD于H,∵AB∥OD,∴△OCF∽△AEF,△ODG∽△AEG,
∴![]() ,
,![]() , 又∵CF+EF=5,DG+EG=4,∴CF=t,EG=
, 又∵CF+EF=5,DG+EG=4,∴CF=t,EG=![]() ,∵FH∥ED,∴
,∵FH∥ED,∴ ![]() ,∴HD=
,∴HD=![]() ·CD=
·CD=![]() (5-t )
(5-t )
∴S= ![]() EG·HD=
EG·HD=![]() ×
×![]() ×
×![]() (5-t )=
(5-t )=![]() (5-t )2(0≤t≤5)
(5-t )2(0≤t≤5)
(3)①由(2)知CF=t,(i)當CF=CD時,則t=3,(ii)當CF=DF時,則CH=![]() CD,
CD,

∵FH∥ED,∴CF= ![]() CE=
CE= ![]() ,∴t=
,∴t=![]() ;
;
(iii)當DF=CD時,作DK⊥CF于K,則CK=![]() CF=
CF=![]() t,
t,
∵CK=CD·cos∠ECD,∴![]() t=3×
t=3×![]() ,∴t=
,∴t=![]() ;
;
綜上,當t=3或![]() 或
或 ![]() 時,△CDF為等腰三角形;
時,△CDF為等腰三角形;
②能 t=![]() 作FH⊥CD于H,則△FCH∽△ECD,∴
作FH⊥CD于H,則△FCH∽△ECD,∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
若△CDF的外接圓與OA相切,則F點為切點, 由切割線定理,得:OF2=OC![]() OD,
OD,
∴![]() , 解得t=
, 解得t=![]()


科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,E,F分別為AD,BC邊上的一點,增加下列條件,不能得出BE∥DF的是( )
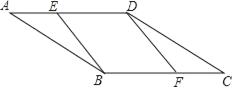
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第五屆中國機器人峰會將于5月9日在余姚開幕,某公司購買一種T恤衫參加此次峰會.了解到某商店正好有這種T恤衫的促銷,當購買10件時每件140元,購買數量每增加1件單價減少1元;當購買數量為60件(含60件)以上時,一律每件80元.
(1)如果購買![]() 件(10<
件(10<![]() <60),每件的單價為
<60),每件的單價為![]() 元,請寫出
元,請寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)如果該公司共購買了100件T恤衫,由于某種原因需分兩批購買,且第一批購買量多于30件且少于60件.已知購買兩批T恤衫一共花了9200元,求第一批T恤衫的購買數量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,則下面的結論:
①△ODC是等邊三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE ,
其中正確結論有( )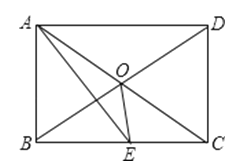
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級(1)班現要從A、B兩位男生和D、E兩位女生中,選派學生代表本班參加全校“中華好詩詞”大賽.
(1)如果選派一位學生代表參賽,那么選派到的代表是A的概率 ;
(2)如果選派兩位學生代表參賽,求恰好選派一男一女兩位同學參賽的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AE平分∠BAD,交BC于點E,BF平分∠ABC,交AD于點F,AE與BF交于點P,連接EF,PD.
(1)求證:四邊形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片ABCD,使AD落在BD上,點A恰好與BD上的點F重合.展開后,折痕DE分別交AB、AC于點E、G.連接GF.下列結論:①∠AGD=112.5°;②AD:AE=2;③S△AGD=S△OGD;④四邊形AEFG是菱形;⑤BE=2 OG。其中正確結論的序號是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先化簡,再求值:
(1)3x+2(x2-y)-3(2x2+x-![]() y),其中x=
y),其中x=![]() ,y=-3;
,y=-3;
(2)3a2c-[2ab2-2(abc-![]() ab2)+3a2c]-abc,其中a=-
ab2)+3a2c]-abc,其中a=-![]() ,b=2,c=3.
,b=2,c=3.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com