
(本題滿分12分)在平面直角坐標系中,拋物線y=x2+(k﹣1)x﹣k與直線y=kx+1交于A,B兩點,點A在點B的左側.

(1)如圖1,當k=1時,直接寫出A,B兩點的坐標;
(2)在(1)的條件下,點P為拋物線上的一個動點,且在直線AB下方,試求出△ABP面積的最大值及此時點P的坐標;
(3)如圖2,拋物線y=x2+(k﹣1)x﹣k(k>0)與x軸交于點C、D兩點(點C在點D的左側),在直線y=kx+1上是否存在唯一一點Q,使得∠OQC=90°?若存在,請求出此時k的值;若不存在,請說明理由.
(1)A(﹣1,0),B(2,3);(2)△ABP面積最大值為 ,此時點P坐標為(
,此時點P坐標為( ,﹣
,﹣ );(3)
);(3)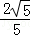 或1.
或1.
【解析】
試題分析:(1)當k=1時,聯立拋物線與直線的解析式,解方程求得點A、B的坐標;
(2)如答圖2,作輔助線,求出△ABP面積的表達式,然后利用二次函數的性質求出最大值及點P的坐標;
(3)“存在唯一一點Q,使得∠OQC=90°”的含義是,以OC為直徑的圓與直線AB相切于點Q,由圓周角定理可證,此時∠OQC=90°且點Q為唯一.以此為基礎,構造相似三角形,利用比例式列出方程,求得k的值,注意另外注意一點是考慮直線AB是否與拋物線交于C點,此時亦存在唯一一點Q,使得∠OQC=90°.
試題解析:解:(1)當k=1時,拋物線解析式為y=x2﹣1,直線解析式為y=x+1.
聯立兩個解析式,得:x2﹣1=x+1,
解得:x=﹣1或x=2,
當x=﹣1時,y=x+1=0;當x=2時,y=x+1=3,
∴A(﹣1,0),B(2,3).
(2)設P(x,x2﹣1).
如答圖2所示,過點P作PF∥y軸,交直線AB于點F,則F(x,x+1).
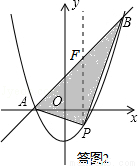
∴PF=yF﹣yP=(x+1)﹣(x2﹣1)=﹣x2+x+2.
S△ABP=S△PFA+S△PFB= ,
,
∴S△ABP= (﹣x2+x+2)=﹣
(﹣x2+x+2)=﹣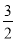 (x﹣
(x﹣ )2+
)2+
當x= 時,yP=x2﹣1=﹣
時,yP=x2﹣1=﹣ .
.
∴△ABP面積最大值為 ,此時點P坐標為(
,此時點P坐標為( ,﹣
,﹣ ).
).
(3)設直線AB:y=kx+1與x軸、y軸分別交于點E、F,
則E(﹣ ,0),F(0,1),OE=
,0),F(0,1),OE= ,OF=1.
,OF=1.
在Rt△EOF中,由勾股定理得:EF= =
= .
.
令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1.
∴C(﹣k,0),OC=k.
Ⅰ、假設存在唯一一點Q,使得∠OQC=90°,如答圖3所示,
則以OC為直徑的圓與直線AB相切于點Q,根據圓周角定理,此時∠OQC=90°.

設點N為OC中點,連接NQ,則NQ⊥EF,NQ=CN=ON=.
∴EN=OE﹣ON=﹣.
∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,
∴△EQN∽△EOF,
∴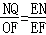 ,即:
,即: ,
,
解得:k=±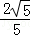 ,
,
∵k>0,
∴k=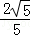 .
.
∴存在唯一一點Q,使得∠OQC=90°,此時k=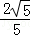 .
.
Ⅱ、若直線AB過點C時,此時直線與圓的交點只有另一點Q點,故亦存在唯一一點Q,使得∠OQC=90°,
將C(﹣k,0)代入y=kx+1中,可得k=1,k=-1(舍去),
故亦存在唯一一點Q,使得∠OQC=90°,此時k=1.
綜上所述,k=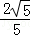 或1時,存在唯一一點Q,使得∠OQC=90°.
或1時,存在唯一一點Q,使得∠OQC=90°.
考點:二次函數綜合題;一次函數的圖象與性質;直線與圓的位置關系.
考點分析: 考點1:二次函數 定義: (a,b,c是常數,a≠0),那么y叫做x 的二次函數。
(a,b,c是常數,a≠0),那么y叫做x 的二次函數。  (a≠0)中x、y是變量,a,b,c是常數,自變量x 的取值范圍是全體實數,b和c可以是任意實數,a是不等于0的實數,因為a=0時,
(a≠0)中x、y是變量,a,b,c是常數,自變量x 的取值范圍是全體實數,b和c可以是任意實數,a是不等于0的實數,因為a=0時, 變為y=bx+c若b≠0,則y=bx+c是一次函數,若b=0,則y=c是一個常數函數。
變為y=bx+c若b≠0,則y=bx+c是一次函數,若b=0,則y=c是一個常數函數。 (a≠0)與一元二次方程
(a≠0)與一元二次方程 (a≠0)有密切聯系,如果將變量y換成一個常數,那么這個二次函數就是一個一元二次函數。
二次函數的解析式有三種形式:
(a≠0)有密切聯系,如果將變量y換成一個常數,那么這個二次函數就是一個一元二次函數。
二次函數的解析式有三種形式:  (a,b,c是常數,a≠0);
(a,b,c是常數,a≠0);  (a,h,k是常數,a≠0)
(a,h,k是常數,a≠0)  與x軸有交點時,即對應二次好方程
與x軸有交點時,即對應二次好方程 有實根x1和x2存在時,根據二次三項式的分解因式
有實根x1和x2存在時,根據二次三項式的分解因式 ,二次函數
,二次函數 可轉化為兩根式
可轉化為兩根式 。如果沒有交點,則不能這樣表示。
。如果沒有交點,則不能這樣表示。  (a≠0)的形式,那么這個函數就是二次函數,否則就不是。
試題屬性
(a≠0)的形式,那么這個函數就是二次函數,否則就不是。
試題屬性


科目:初中數學 來源:2014-2015學年安徽省七年級下學期開學考試數學試卷(解析版) 題型:解答題
(10分)把一副三角板的直角頂點O重疊在一起,
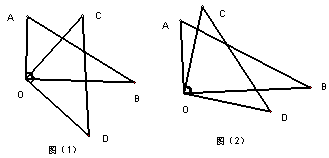
(1)如圖(1),當OB平分∠COD時,則∠AOD和∠BOC的和是多少度?
(2)如圖(2),當OB不平分∠COD時,則∠AOD和∠BOC的和是多少度?
(3)當∠BOC的余角的4倍等于∠AOD,則∠BOC多少度?
查看答案和解析>>
科目:初中數學 來源:2014-2015學年安徽省八年級下學期開學考試數學試卷(解析版) 題型:選擇題
一個凸多邊形的每一內角都等于140°,那么從這個多邊形的一個頂點出發的對角線的條數是( )
A.9條 B.8條 C.7條 D.6條
查看答案和解析>>
科目:初中數學 來源:2014-2015學年陜西省西安市九年級下學期第一次月考數學試卷(解析版) 題型:填空題
如圖,點A,B的坐標分別為(1, 4)和(4, 4),拋物線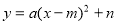 的頂點在線段AB上運動,與x軸交于C、D兩點(C在D的左側),點C的橫坐標最小值為
的頂點在線段AB上運動,與x軸交于C、D兩點(C在D的左側),點C的橫坐標最小值為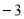 ,則點D的橫坐標最大值為_______。
,則點D的橫坐標最大值為_______。

查看答案和解析>>
科目:初中數學 來源:2014-2015學年陜西省西安市九年級下學期第一次月考數學試卷(解析版) 題型:選擇題
西安火車站的顯示屏每隔4分鐘顯示一次火車車次的信息,顯示時間持續1分鐘,某人到達火車站時,顯示屏正好顯示火車車次信息的概率是( )
A.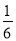 B.
B.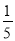 C.
C.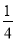 D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市第一教研片九年級下學期第一次月考數學試卷(解析版) 題型:解答題
23.(本題滿分10分)如圖,在菱形ABCD中,AB=2,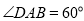 ,點E是AD邊的中點,點M是AB邊上一動點(不與點A重合),延長ME交射線CD于點N,連接MD,AN.
,點E是AD邊的中點,點M是AB邊上一動點(不與點A重合),延長ME交射線CD于點N,連接MD,AN.
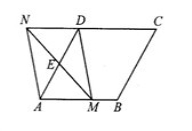
(1)求證:四邊形AMDN是平行四邊形;
(2)填空:①當AM的值為 時,四邊形AMDN是矩形;
②當AM的值為 時,四邊形AMDN是菱形.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省東臺市第一教研片九年級下學期第一次月考數學試卷(解析版) 題型:填空題
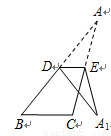
如圖,在 中,
中, 、
、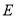 分別是邊
分別是邊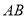 、
、 的中點,
的中點, .現將
.現將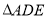 沿
沿 折疊,點
折疊,點 落在三角形所在平面內的點為
落在三角形所在平面內的點為 ,則
,則 的度數為 °.
的度數為 °.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省九年級3月聯考數學試卷(解析版) 題型:解答題
(本題10分)如圖1,梯形ABCD中AB∥CD,且AB=2CD,點P為BD的中點,直線AP交BC于E,交DC的延長線于F.
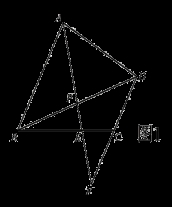
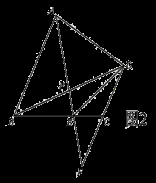
(1)求證:DC=CF;
(2)求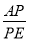 的值;
的值;
(3)如圖2,連接DE,若AD⊥ED,求證: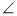 BAE=
BAE=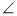 DBE.
DBE.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省九年級3月聯考數學試卷(解析版) 題型:選擇題
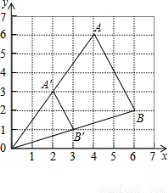
如圖,△ABO縮小后變為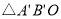 ,其中A、B的對應點分別為
,其中A、B的對應點分別為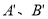 ,
,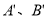 均在圖中格點上,若線段AB上有一點
均在圖中格點上,若線段AB上有一點 ,則點
,則點 在
在 上的對應點
上的對應點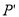 的坐標為( ).
的坐標為( ).
A、 B、
B、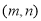 C、
C、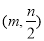 D、
D、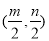
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com