
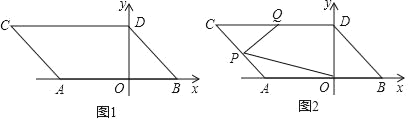
【題目】如圖1,在平面直角坐標系中,點A,B的坐標分別為A(a,0),B(b,0),且a,b滿足|2a+6|+(2a﹣3b+12)2=0,現同時將點A,B分別向左平移2個單位,再向上平移2個單位,分別得到點A,B的對應點C,D,連接AC,BD.
(1)請直接寫出A,B兩點的坐標;
(2)如圖2,點P是線段AC上的一個動點,點Q是線段CD的中點,連接PQ,PO,當點P在線段AC上移動時(不與A,C重合),請找出∠PQD,∠OPQ,∠POB的數量關系,并證明你的結論;
(3)在坐標軸上是否存在點M,使三角形MAD的面積與三角形ACD的面積相等?若存在,直接寫出點M的坐標;若不存在,試說明理由.
【答案】(1)A(﹣3,0),B(2,0);(2)∠PQD+∠OPQ+∠POB=360°,理由見解析;(3)三角形MAD的面積與三角形ACD的面積相等時,點M的坐標為(2,0)或(﹣8,0)或(0,﹣![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)根據絕對值的非負性、偶次方的非負性分別求出a、b,得到點A,B的坐標;
(2)求出五邊形QPOBD的內角和,根據平行線的性質得到∠QDB+∠OBD=180°,計算即可;
(3)根據題意求出△ACD的面積,分點M在x軸上、點M在y軸上兩種情況,根據三角形的面積公式計算即可.
解:(1)∵|2a+6|+(2a﹣3b+12)2=0,
∴|2a+6|=0,(2a﹣3b+12)2=0,
解得,a=﹣3,b=2,
則點A,B的坐標分別為A(﹣3,0),B(2,0);
(2)∠PQD+∠OPQ+∠POB=360°,
理由如下:五邊形QPOBD的內角和=(5﹣2)×180°=540°,
∵CD∥AB,
∴∠QDB+∠OBD=180°,
∴∠PQD+∠OPQ+∠POB=540°﹣(∠QDB+∠OBD)=360°;
(3)由題意得,點C的坐標為(﹣5,2),點D的坐標為(0,2),
則△ACD的面積=![]() ×5×2=5,
×5×2=5,
當點M在x軸上時,設點M的坐標為(x,0),
則AM=|﹣3﹣x|,
由題意得,![]() ×|﹣3﹣x|×2=5,
×|﹣3﹣x|×2=5,
解得,x=2或﹣8,
當點M在y軸上時,設點M的坐標為(0,y),
則AM=|2﹣y|,
由題意得,![]() ×|2﹣y|×3=5,
×|2﹣y|×3=5,
解得,y=﹣![]() 或
或![]() ,
,
綜上所述,三角形MAD的面積與三角形ACD的面積相等時,點M的坐標為(2,0)或(﹣8,0)或(0,﹣![]() )或(0,
)或(0,![]() ).
).


科目:初中數學 來源: 題型:
【題目】某校為了解學生體質情況,從各年級隨機抽取部分學生進行體能測試,每個學生的測試成績按標準對應為優秀、良好、及格、不及格四個等級.統計員在將測試數據繪制成圖表時發現,優秀漏統計![]() 人,良好漏統計
人,良好漏統計![]() 人,于是及時更正,從而形成如下圖表.請按正確數據解答下列各題:
人,于是及時更正,從而形成如下圖表.請按正確數據解答下列各題:
(1)填寫統計表.
(2)根據調整后數據,補全條形統計圖.
(3)若該校共有學生![]() 人,請你估算出該校體能測試等級為“優秀”的人數.
人,請你估算出該校體能測試等級為“優秀”的人數.
學生體能測試成績各等次人數統計表
體能等級 | 調整前人數 | 調整后人數 |
優秀 |
| |
良好 |
| |
及格 |
| |
不及格 |
| |
合計 |
|
學生體能測試成績各等次人數統計圖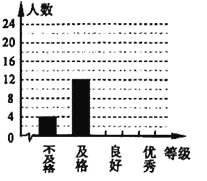
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D是BC邊上的一點,∠B=50°,∠BAD=30°,將△ABD沿AD折疊得到△AED,AE與BC交于點F.
(1)填空:∠ADC= 度;
(2)當∠C=20°時,判斷DE與AC的位置關系,并說明理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
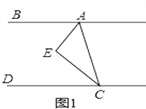
(1)請判斷AB與CD的位置關系并說明理由;
(2)如圖2,在(1)的結論下,當∠E=90°保持不變,移動直角頂點E,使∠MCE=∠ECD,當直角頂點E點移動時,問∠BAE與∠MCD是否存在確定的數量關系?

(3)如圖3,在(1)的結論下,P為線段AC上一定點,點Q為直線CD上一動點,當點Q在射線CD上運動時(點C除外)∠CPQ+∠CQP與∠BAC有何數量關系? (2、3小題只需選一題說明理由)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖棱長為a的小正方體,按照下圖的方法繼續擺放,自上而下分別叫第一層。第二層……第n層,第n層的小正方體的個數記為S.解答下列問題:
(1)填寫表格:
n | 1 | 2 | 3 | 4 | … |
S | 1 |
| … |
(2)研究上表可以發現S隨n的變化而變化,且S隨n的增大而增大有一定的規律,請你用式子來表示S與n的關系,并計算當n=10時,S的值為多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下列證明:如圖,已知AD⊥BC,EF⊥BC,∠1=∠2.
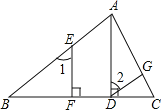
求證:DG∥BA.
證明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=90°,∠ADB=90°(______)
∴∠EFB=∠ADB(等量代換)
∴EF∥AD(______)
∴∠1=∠BAD(______)
又∵∠1=∠2(已知)
∴∠______=∠______(等量代換)
∴DG∥BA.(______).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用配方法解下列方程時,配方有錯誤的是( )
A.x2﹣2x﹣99=0化為(x﹣1)2=100
B.x2+8x+9=0化為(x+4)2=25
C.2t2﹣7t﹣4=0化為(t﹣ ![]() )2=
)2= ![]()
D.3x2﹣4x﹣2=0化為(x﹣ ![]() )2=
)2= ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com