
【題目】如圖棱長為a的小正方體,按照下圖的方法繼續擺放,自上而下分別叫第一層。第二層……第n層,第n層的小正方體的個數記為S.解答下列問題:
(1)填寫表格:
n | 1 | 2 | 3 | 4 | … |
S | 1 |
| … |
(2)研究上表可以發現S隨n的變化而變化,且S隨n的增大而增大有一定的規律,請你用式子來表示S與n的關系,并計算當n=10時,S的值為多少?

 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案科目:初中數學 來源: 題型:
【題目】我們給出如下定義:順次連接任意一個四邊形各邊中點所得的四邊形叫中點四邊形.

(1)如圖1,四邊形ABCD中,點E,F,G,H分別為邊AB,BC,CD,DA的中點.求證:中點四邊形EFGH是平行四邊形;
(2)如圖2,點P是四邊形ABCD內一點,且滿足PA=PB,PC=PD,∠APB=∠CPD,點E,F,G,H分別為邊AB,BC,CD,DA的中點,猜想中點四邊形EFGH的形狀,并證明你的猜想;
(3)若改變(2)中的條件,使∠APB=∠CPD=90°,其他條件不變,直接寫出中點四邊形EFGH的形狀.(不必證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列一組圖形中的個數,其中第1個圖中共有4個點,第2個圖中共有10個點,第3個圖中共有19個點,……,按此規律第5個圖中共有點的個數是( )

A. 31 B. 46 C. 51 D. 66
查看答案和解析>>
科目:初中數學 來源: 題型:
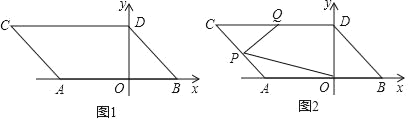
【題目】如圖1,在平面直角坐標系中,點A,B的坐標分別為A(a,0),B(b,0),且a,b滿足|2a+6|+(2a﹣3b+12)2=0,現同時將點A,B分別向左平移2個單位,再向上平移2個單位,分別得到點A,B的對應點C,D,連接AC,BD.
(1)請直接寫出A,B兩點的坐標;
(2)如圖2,點P是線段AC上的一個動點,點Q是線段CD的中點,連接PQ,PO,當點P在線段AC上移動時(不與A,C重合),請找出∠PQD,∠OPQ,∠POB的數量關系,并證明你的結論;
(3)在坐標軸上是否存在點M,使三角形MAD的面積與三角形ACD的面積相等?若存在,直接寫出點M的坐標;若不存在,試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
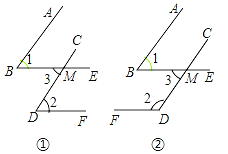
【題目】已知一個角的兩邊與另一個角的兩邊分別平行,請結合圖,探索這兩個角之間的關系,并說明理由.
(1)如圖①,AB∥CD,BE∥DF,∠1與∠2的關系是 ;
證明:
(2)如圖②,AB∥CD,BE∥DF,∠1與∠2的關系是 ;
證明:
(3)經過上述證明,我們可得出結論,如果一個角的兩邊與另一個角的兩邊分別平行,那么這兩個角 ;
(4)若這兩個角的兩邊分別平行,且一個角比另一個角的3倍少60°,則這兩個角分別是多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
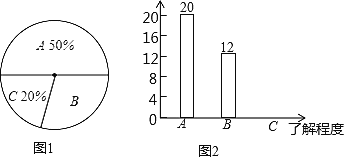
【題目】雙峰縣教育局要求各學校加強對學生的安全教育,全縣各中小學校引起高度重視,小剛就本班同學對安全知識的了解程度進行了一次調查統計.他將統計結果分為三類,A:熟悉;B:了解較多;C:一般了解。圖①和圖②是他采集數據后,繪制的兩幅不完整的統計圖,請你根據圖中提供的信息解答以下問題:
(1)求小剛所在的班級共有多少名學生;
(2)在條形圖中,將表示“一般了解”的部分補充完整‘’
(3)在扇形統計圖中,計算“了解較多”部分所對應的扇形圓心角的度數;
(4)如果小剛所在年級共1000名同學,請你估算全年級對安全知識“了解較多”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數![]() 都可以進行這樣的分解:
都可以進行這樣的分解:![]() (
(![]() 是正整數,且
是正整數,且![]() ),在
),在![]() 的所有這種分解中,如果
的所有這種分解中,如果![]() 兩因數之差的絕對值最小,我們就稱
兩因數之差的絕對值最小,我們就稱![]() 是
是![]() 的最佳分解并規定:
的最佳分解并規定:![]() ,例如:12可以分解成1×12、2×6、3×4,因為:
,例如:12可以分解成1×12、2×6、3×4,因為:
![]() ,所以3×4是12的最佳分解,所以F(12)=
,所以3×4是12的最佳分解,所以F(12)=![]()
(1)求F(18)-F(16)的值;
(2)若正整數![]() 是4的倍數,我們稱正整數
是4的倍數,我們稱正整數![]() 為“四季數”,如果一個兩位正整數
為“四季數”,如果一個兩位正整數![]()
![]() (
(![]() ,
,![]() 為自然數),交換個位上的數字與十位上的數字得到的新兩位正整數減去原來的兩位正整數所得的差為“四季數”,那么我們稱這個數
為自然數),交換個位上的數字與十位上的數字得到的新兩位正整數減去原來的兩位正整數所得的差為“四季數”,那么我們稱這個數![]() 為“有緣數”,求所有“有緣數”中
為“有緣數”,求所有“有緣數”中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學在今年4月23日的“世界讀書日”開展“人人喜愛閱讀,爭當閱讀能手”活動,同學們積極響應,涌現出大批的閱讀能手.為了激勵同學們的閱讀熱情,養成每天閱讀的好習慣,學校對閱讀能手進行了獎勵表彰,計劃用2700元來購買甲、乙、丙三種書籍共100本作為獎品,已知甲、乙、丙三種書的價格比為2:2:3,甲種書每本20元.
(1)求出乙、丙兩種書的每本各多少元?
(2)若學校購買甲種書的數量是乙種書的1.5倍,恰好用完計劃資金,求甲、乙、丙三種書各買了多少本?
(3)在活動中,同學們表現優秀,學校決定提升獎勵檔次,增加了245元的購書款,在購買書籍總數不變的情況下,求丙種書最多可以買多少本?
(4)七(1)班閱讀氛圍濃厚,同伴之間交換書籍共享閱讀,已知甲種書籍共270頁,小明同學閱讀甲種書籍每天21頁,閱讀5天后,發現同伴比他看得快,為了和同伴及時交換書籍,接下來小明每天多讀了a頁(20<a<40),結果再用了b天讀完,求小明讀完整本書共用了多少天?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com