
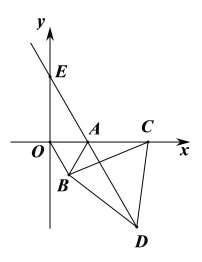
【題目】如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,以線段
,以線段![]() 為邊在第四象限內作等邊三角形
為邊在第四象限內作等邊三角形![]() ,點
,點![]() 為
為![]() 正半軸上一動點
正半軸上一動點![]() , 連接
, 連接![]() ,以線段
,以線段![]() 為邊在第四象限內作等邊三角形
為邊在第四象限內作等邊三角形![]() ,連接
,連接![]() 并延長,交
并延長,交![]() 軸于點
軸于點![]() .
.
(1)求證:![]() ≌
≌![]() ;
;
(2)在點![]() 的運動過程中,
的運動過程中,![]() 的度數是否會變化?如果不變,請求出
的度數是否會變化?如果不變,請求出![]() 的度數;如果變化,請說明理由.
的度數;如果變化,請說明理由.
(3)當點![]() 運動到什么位置時,以
運動到什么位置時,以![]() 為頂點的三角形是等腰三角形?
為頂點的三角形是等腰三角形?
【答案】![]() 詳見解析;
詳見解析;![]() 的度數不會變化,
的度數不會變化,![]() ;
;![]() 當點
當點![]() 運動到
運動到![]() 時.
時.
【解析】
(1)根據等邊三角形的性質可得BO=BA,BC=BD,∠OBA=∠CBD=60°,進而可利用SAS證明![]() ≌
≌![]() ;
;
(2)設BC、DE交于點F,如圖1,根據全等三角形的性質可得∠1=∠2,根據三角形的內角和定理可得∠CAD=∠CBD,進而可得結論;
(3)易求得∠EAC=120°,∠OEA=30°,即得以A,E,C為頂點的三角形是等腰三角形時,AE和AC是腰,然后根據30°角的直角三角形的性質可得AE的長,進而可得AC、OC的長,即可得出點C的位置.
解:(1)證明:∵△AOB、△BCD是等邊三角形,
∴BO=BA,BC=BD,∠OBA=∠CBD=60°,
∴∠OBC=∠ABD,
∴![]() ≌
≌![]() (SAS);
(SAS);
(2)設BC、DE交于點F,如圖1,
∵![]() ≌
≌![]() ,∴∠1=∠2,
,∴∠1=∠2,
∵∠AFC=∠BFD,∴∠CAD=∠CBD=60°,
∴![]() 的度數不會變化,且
的度數不會變化,且![]() ;
;

(3)∵![]() ,∴∠EAC=120°,∠OAE=60°,∴∠OEA=30°,
,∴∠EAC=120°,∠OAE=60°,∴∠OEA=30°,
∴以A,E,C為頂點的三角形是等腰三角形時,AE和AC是腰,
∵在Rt△AOE中,OA=1,∠OEA=30°,∴AE=2,
∴AC=AE=2,∴OC=1+2=3,
∴當點C的坐標為(3,0)時,以A,E,C為頂點的三角形是等腰三角形.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC=10,BC=16,AD是BC邊上的中線且AD=6,![]() 是AD上的動點,
是AD上的動點,![]() 是AC邊上的動點,則
是AC邊上的動點,則![]() 的最小值是( ).
的最小值是( ).

A.![]() B.16C.6D.10
B.16C.6D.10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,A(-2,1),B(-3,4),C(-1,3),過點(l,0)作x軸的垂線![]() .
.
(1)作出△ABC關于直線![]() 的軸對稱圖形△
的軸對稱圖形△![]() ;
;
(2)直接寫出A1(___,___),B1(___,___),C1(___,___);
(3)在△ABC內有一點P(m,n),則點P關于直線![]() 的對稱點P1的坐標為(___,___)(結果用含m,n的式子表示).
的對稱點P1的坐標為(___,___)(結果用含m,n的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店老板去圖書批發市場購買某種圖書,第一次用![]() 元購書若干本, 并按該書定價
元購書若干本, 并按該書定價![]() 元出售,很快售完.由于該書暢銷,第二次購書時,每本書的批發價已比第一次提高了
元出售,很快售完.由于該書暢銷,第二次購書時,每本書的批發價已比第一次提高了![]() ,他用
,他用![]() 元所購該書數量比第一次多
元所購該書數量比第一次多![]() 本.當按定價
本.當按定價![]() 元售出
元售出![]() 本時,出現滯銷,便以定價的
本時,出現滯銷,便以定價的![]() 折售完剩余的書.
折售完剩余的書.
![]() 每本書第一次的批發價是多少錢?
每本書第一次的批發價是多少錢?
![]() 試問該老板這兩次售書總體上是賠錢了,還是賺錢了(不考慮其它因素)?若賠錢,賠多少?若賺錢,賺多少?
試問該老板這兩次售書總體上是賠錢了,還是賺錢了(不考慮其它因素)?若賠錢,賠多少?若賺錢,賺多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】材料:我們將能完全覆蓋三角形的最小圓稱為該三角形的最小覆蓋圓.若三角形為銳角三角形,則其最小覆蓋圓為其外接圓;若三角形為直角或鈍角三角形,則其最小覆蓋圓是以三角形最長邊(直角或鈍角所對的邊)為直徑的圓.問題:能覆蓋住邊長為![]() 、
、![]() 、
、![]() 的三角形的最小圓的直徑是________.
的三角形的最小圓的直徑是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
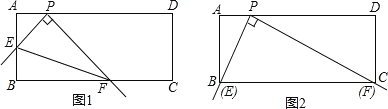
【題目】在矩形ABCD中,點P在AD上,AB=![]() ,AP=1.將直角尺的頂點放在P處,直角尺的兩邊分別交AB、BC于點E、F,連接EF(如圖1).當點E與點B重合時,點F恰好與點C重合(如圖2).將直角尺從圖2中的位置開始,繞點P順時針旋轉,當點E和點A重合時停止.在這個過程中,從開始到停止,線段EF的中點所經過的路徑長為.
,AP=1.將直角尺的頂點放在P處,直角尺的兩邊分別交AB、BC于點E、F,連接EF(如圖1).當點E與點B重合時,點F恰好與點C重合(如圖2).將直角尺從圖2中的位置開始,繞點P順時針旋轉,當點E和點A重合時停止.在這個過程中,從開始到停止,線段EF的中點所經過的路徑長為.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寒假即將到來,外出旅游的人數逐漸增多,對旅行包的需求也將增多,某店準備到生產廠家購買旅行包,該廠有甲、乙兩種新型旅行包.若購進10個甲種旅行包和20個乙種旅行包共需5600元,若購進20個甲種旅行包和10個乙種旅行包共需5200元.
(1)甲、乙兩種旅行包的進價分別是多少元?
(2)若該店恰好用了7000元購買旅行包;
①設該店購買了m個甲種旅行包,求該店購買乙種旅行包的個數;
②若該店將甲種旅行包的售價定為298元,乙種旅行包的售價定為325元,則當該店怎么樣進貨,才能獲得最大利潤,并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com