
【題目】(1)探究:
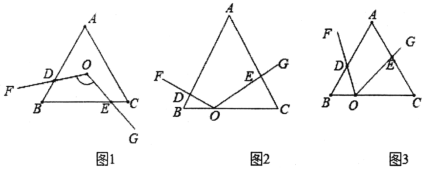
問題:如圖1,等邊三角形ABC的邊長為6,點O是∠ABC和∠ACB的角平分線交點,∠FOG=120°,繞點O任意旋轉∠FOG,分別交△ABC的兩邊于D,E兩點求四邊形ODBE的面積.
討論:
①甲:在∠FOG旋轉過程中,當OF經過點B時,OG一定經過點C.
②乙:小明的分析有道理,這樣,我們就可以利用“ASA”證出△ODB≌△OEC.
③丙:因為△ODB≌△OEC,所以只要算出△OBC的面積就得出了四邊形ODBE的面積.
老師:同學們的思路很清晰,也很正確,在分析和解決問題時,我們經常會借用特例作輔助線來解決一般問題請你按照探究的思路,直接寫出四邊形ODBE的面積:________.
(2)應用:
①特例:如圖2,∠FOG的頂點O在等邊三角形ABC的邊BC上,OB=2,OC=4,邊OG⊥AC于點E,OF⊥AB于點D,求△BOD面積.
②探究:如圖3,已知∠FOG=60°,頂點O在等邊三角形ABC的邊BC上,OB=2,OC=4,記△BOD的面積為x,△COE的面積為y,求xy的值.
【答案】探究:3![]() ;應用:①
;應用:①![]() ;②12.
;②12.
【解析】
(1)(1)由“ASA”可證△DOB≌△EOC,可得S△DOB=S△EOC,可得S△OBC=四邊形ODBE的面積,即可求解;
(2)①由直角三角形的性質可求OD,BD的長,即可求解;
②過點O作OM⊥AB于M,ON⊥AC于N,可求OM=![]() ,ON=2
,ON=2![]() ,通過證明△BDO∽△COE,可得
,通過證明△BDO∽△COE,可得![]() =
=![]() ,可得BDEC=OBOC=8,即可求解;
,可得BDEC=OBOC=8,即可求解;
解:(1)方法引導:
如圖1,連接OB,OC,
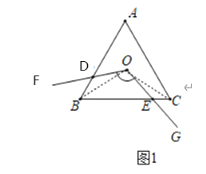
∵△ABC是等邊三角形,
∴∠ABC=∠ACB=60°,
∵點O是∠ABC和∠ACB的角平分線交點,
∴∠ABO=∠OBC=∠OCB=30°,
∴OB=OC,∠BOC=∠FOG=120°,
∴∠DOB=∠COE,且OB=OC,∠ABO=∠BCO,
∴△DOB≌△EOC(ASA)
∴S△DOB=S△EOC,
∴S△OBC=四邊形ODBE的面積,
∵等邊三角形ABC的邊長為6,
∴S△ABC=![]() ×62=9
×62=9![]() ,
,
∴S△OBC=四邊形ODBE的面積=![]() S△ABC=3
S△ABC=3![]() ,
,
故答案為:3![]() ;
;
(2)①∵△ABC是等邊三角形,∠B=60°,
∵OF⊥AB,
∴∠BOD=30°,
∵OB=2,
∴BD=1,
∴OD=![]() ,
,
∴△BOD的面積=![]() ×1×
×1×![]() =
=![]() ;
;
②過點O作OM⊥AB于M,ON⊥AC于N,
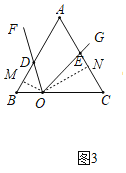
由①得:OM=![]() ,同理:ON=2
,同理:ON=2![]() ,
,
∵△ABC是等邊三角形,
∴∠B=∠C=60°,
∵∠DOC=∠B+∠BDO=∠DOG+∠COG,且∠FOG=60°,
∴∠COG=∠BDO,且∠B=∠C=60°,
∴△BDO∽△COE,
∴![]() =
=![]() ,
,
∴BDEC=OBOC=8,
∴xy=![]() ×BD×
×BD×![]() ×
×![]() ×CE×2
×CE×2![]() =12;
=12;


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C、G是⊙O上兩點,且![]() ,過點C的直線CD
,過點C的直線CD![]() BG于點D,交BA的延長線于點E,連接BC,交OD于點F.
BG于點D,交BA的延長線于點E,連接BC,交OD于點F.
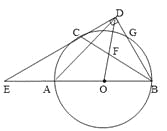
(1)求證:CD是⊙O的切線.
(2)若![]() ,求
,求![]() E的度數.
E的度數.
(3)連接AD,在(2)的條件下,若CD=![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在直角坐標系中,(為坐標原點,點![]() ,點
,點![]() 是
是![]() 中點,連接(
中點,連接(![]() 將
將![]() 繞點
繞點![]() 順時針旋轉,得到
順時針旋轉,得到![]() ,記旋轉角為
,記旋轉角為![]() ,點
,點![]() 的對應點分別是
的對應點分別是![]() ,連接
,連接![]() 是
是![]() 中點,連接
中點,連接![]() .
.
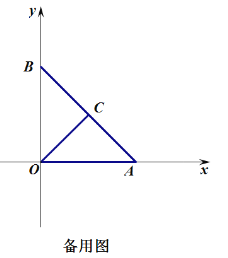
(1)如圖①,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;

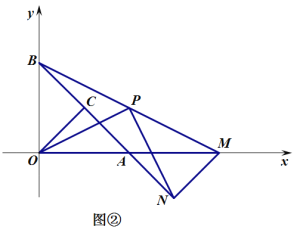
(2)如圖②,當![]() 時,求證
時,求證![]() ,且
,且![]() ;
;
(3)當![]() 旋轉至點
旋轉至點![]() 共線時,求點
共線時,求點![]() 的坐標(直接寫出結果即可) .
的坐標(直接寫出結果即可) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的方程(2m+1)x2+4mx+2m﹣3=0有兩個不相等的實數根.
(1)求m的取值范圍;
(2)是否存在實數m,使方程的兩個實數根的倒數之和等于﹣1?若存在,求出m的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
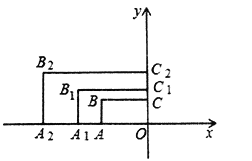
【題目】如圖,在平面直角坐標系中,矩形AOCB的兩邊OA、OC分別在x軸和y軸上,且OA=2,OC=1.在第二象限內,將矩形AOCB以原點O為位似中心放大為原來的![]() 倍,得到矩形A1OC1B1,再將矩形A1OC1B1以原點O為位似中心放大
倍,得到矩形A1OC1B1,再將矩形A1OC1B1以原點O為位似中心放大![]() 倍,得到矩形A2OC2B2,以此類推,得到的矩形A2020OC2020B2020的對角線交點的縱坐標為______________.
倍,得到矩形A2OC2B2,以此類推,得到的矩形A2020OC2020B2020的對角線交點的縱坐標為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
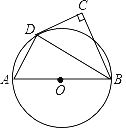
【題目】如圖,AB為⊙O的直徑,點C在⊙O外,∠ABC的平分線與⊙O交于點D,∠C=90°.
(1)求證:CD是⊙O的切線;
(2)若∠CDB=60°,AB=18,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為改善辦學條件,計劃采購A、B兩種型號的空調,已知采購3臺A型空調和2臺B型空調,需費用39000元;4臺A型空調比5臺B型空調的費用多6000元.
(1)求A型空調和B型空調每臺各需多少元;
(2)若學校計劃采購A、B兩種型號空調共30臺,且A型空調的臺數不少于B型空調的一半,兩種型號空調的采購總費用不超過217000元,該校共有哪幾種采購方案?
(3)在(2)的條件下,采用哪一種采購方案可使總費用最低,最低費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育組為了了解九年級450名學生排球墊球的情況,隨機抽查了九年級部分學生進行排球墊球測試(單位:個),根據測試結果,制成了下面不完整的統計圖表:
組別 | 個數段 | 頻數 | 頻率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的數![]() ,
,![]() ;
;
(2)估算該九年級排球墊球測試結果小于10的人數;
(3)排球墊球測試結果小于10的為不達標,若不達標的5人中有3個男生,2個女生,現從這5人中隨機選出2人調查,試通過畫樹狀圖或列表的方法求選出的2人為一個男生一個女生的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com