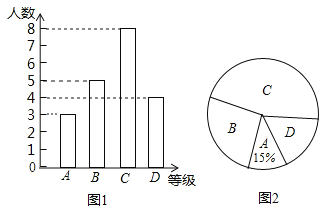
【題目】（10分）“中國夢”關系每個人的幸福生活，為展現巴中人追夢的風采，我市某中學舉行“中國夢我的夢”的演講比賽，賽后整理參賽學生的成績，將學的成績分為A，B，C，D四個等級，并將結果繪制成如圖所示的條形統計圖和扇形統計圖，但均不完整，請你根據統計圖解答下列問題．
（1）參加比賽的學生人數共有 名，在扇形統計圖中，表示“D等級”的扇形的圓心角為 度，圖中m的值為 ；
（2）補全條形統計圖；
（3）組委會決定從本次比賽中獲得A等級的學生中，選出2名去參加市中學生演講比賽，已知A等級中男生有1名，請用“列表”或“畫樹狀圖”的方法求出所選2名學生中恰好是一名男生和一名女生的概率．
【答案】（1）20，72，40；（2）作圖見試題解析；（3）
．
【解析】試題分析：（1）根據等級為A的人數除以所占的百分比求出總人數，根據D級的人數求得D等級扇形圓心角的度數和m的值；
（2）求出等級B的人數，補全條形統計圖即可；
（2）列表得出所有等可能的情況數，找出一男一女的情況數，即可求出所求的概率．
試題解析：（1）根據題意得：3÷15%=20（人），表示“D等級”的扇形的圓心角為
×360°=72°；C級所占的百分比為
×100%=40%，故m=40，故答案為：20，72，40．
（2）故等級B的人數為20﹣（3+8+4）=5（人），
補全統計圖，如圖所示；
（2）列表如下：
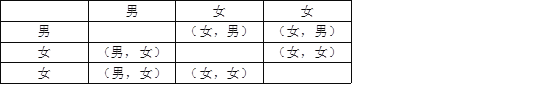
所有等可能的結果有6種，其中恰好是一名男生和一名女生的情況有4種，則P（恰好是一名男生和一名女生）=
=
．
科目：初中數學 來源： 題型：
【題目】初一年級學生在5名教師的帶領下去公園秋游，公園的門票為每人30元，現有兩種優惠方案，甲方案：帶隊教師免費，學生按8折收費；乙方案：師生都7.5折收費.
（1）若有m名學生，用代數式表示兩種優惠方案各需多少元？
（2）當m=70時，采用哪種方案優惠？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,一樓房AB后有一假山,其坡度為i=1∶
,山坡坡面上E點處有一休息亭,測得假山坡腳C與樓房水平距離BC=25米,與亭子距離CE=20米,小麗從樓房頂測得E點的俯角為45°,求樓房AB的高度.(注:坡度i是指坡面的鉛直高度與水平寬度的比)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，數軸的單位長度為1．
（1）如果點A，D表示的數互為相反數，那么點B表示的數是多少？
（2）如果點B，D表示的數互為相反數，那么圖中表示的四個點中，哪一點表示的數的絕對值最大？為什么？
（3）當點B為原點時，若存在一點M到A的距離是點M到D的距離的2倍，則點M所表示的數是____.
查看答案和解析>>
科目：初中數學 來源： 題型：
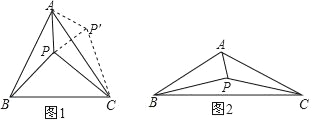
【題目】在△ABC中，AB=AC，∠BAC=α，點P是△ABC內一點，且∠PAC+∠PCA=
，連接PB，試探究PA、PB、PC滿足的等量關系．
（1）當α=60°時，將△ABP繞點A逆時針旋轉60°得到△ACP′，連接PP′，如圖1所示．由△ABP≌△ACP′可以證得△APP′是等邊三角形，再由∠PAC+∠PCA=30°可得∠APC的大小為 度，進而得到△CPP′是直角三角形，這樣可以得到PA、PB、PC滿足的等量關系為 ；
（2）如圖2，當α=120°時，參考（1）中的方法，探究PA、PB、PC滿足的等量關系，并給出證明；
（3）PA、PB、PC滿足的等量關系為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了應對人口老齡化問題，國家大力發展養老事業．某養老機構定制輪椅供行動不便的老人使用．圖①是一種型號的手動輪椅實物圖，圖②為其側面示意圖，該輪椅前后長度為120cm，后輪半徑為24cm，CB=CD=24cm，踏板CB與CD垂直，橫檔AD、踏板CB與地面所成的角分別為15°、30°．求：
（1）求橫檔AD的長；
（2）點C離地面的高度．（sin15°=0.26，cos15°=0.97，精確到1cm）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
