
(10分)如圖1,四邊形ABCD、EFGH為全等的矩形.且矩形ABCD的對角線交于點E,點A在EG上,∠ACB=300.將矩形EFGH繞點E順時針旋轉а角(00<а<600),如圖2,GE、FE與AD分別相交于N、M.
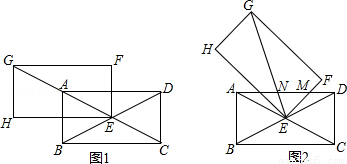
(1)求證:AN+DM>MN;
(2)若MN2+DM2=AN2,求旋轉角а的大小.
(1)證明見試題解析;(2)45°.
【解析】
試題分析:(1)根據矩形的對角線互相平分且相等可得AE=DE,再求出∠AED=120°,將△AEN繞點E順時針旋轉120°得到△DPE,連接MP,根據旋轉的性質可得EP=NE,DP=AN,∠DEP=∠EN,再求出∠MEN=∠MEP=60°,然后利用“邊角邊”證明△MEN和△MEP全等,根據全等三角形對應邊相等可得MN=MP,然后利用三角形的任意兩邊之和大于第三邊證明即可;
(2)利用勾股定理逆定理判斷出△DPM是直角三角形,根據全等三角形對應角相等可得∠EMN=∠EMP=45°,利用三角形的內角和定理求出∠MNE=75°,再根據三角形的一個外角等于與它不相鄰的兩個內角的和求出∠AEN=45°,即為旋轉角度數.
試題解析:(1)∵四邊形ABCD是矩形,∴AE=DE,
∵∠ACB=30°,∴∠AED=180°﹣30°×2=120°,
將△AEN繞點E順時針旋轉120°得到△DPE,連接MP,
則EP=NE,DP=AN,∠DEP=∠EN,
∵∠AED=120°,∴∠MEN=∠MEP=60°,
在△MEN和△MEP中,
∵EP=NE,∠MEN=∠MEP,EM=EM,∴△MEN≌△MEP(SAS),∴MN=MP,
由三角形的三邊關系得,DP+DM>MP,∴AN+DM>MN;
(2)【解析】
∵MN2+DM2=AN2,∴△DPM是直角三角形,∠DMP=90°,
∵△MEN≌△MEP,∴∠EMN=∠EMP=45°,
在△MNE中,∠MNE=180°﹣45°﹣60°=75°,
在△ANE中,∠AEN=∠MNE﹣∠CAD=75°﹣30°=45°,
∴旋轉角為45°.
考點:旋轉的性質.
考點分析: 考點1:圖形的平移與旋轉 定義:

 考前必練系列答案
考前必練系列答案科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期第一次摸底數學試卷(解析版) 題型:解答題
(10分)張明、王成兩位同學初二一學年10次數學單元自我檢測的成績(成績均為整數,且個位數為0)分別如下圖所示:利用圖中提供的信息,解答下列問題.
(1)完成下表
姓名 | 平均成績 | 中位數 | 眾數 | 方差(S2) |
張明 | 80 | 80 | ||
王成 | 260 |
(2)如果將90分以上(含90分)的成績視為A等,則獲得成績為A等多的同學是 ;
(3)根據圖表信息,請你對這位兩同學各提一條不超過20個字的學習建議,并說明提出建議的原因.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年河南省平頂山市九年級上學期第一次月考數學試卷(解析版) 題型:選擇題
如果關于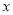 的一元二次方程
的一元二次方程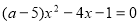 有實數根,則
有實數根,則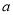 滿足條件是( )
滿足條件是( )
A、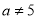 B、
B、 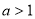 且
且 C、.
C、. 且
且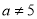 D、
D、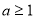
查看答案和解析>>
科目:初中數學 來源:2014-2015學年河南平頂山四十三中八年級上學期第一次段測數學試卷(解析版) 題型:填空題
某農舍的大門是一個木制的矩形柵欄,它的高為4m,寬為3m,現需要在相對的頂點間用一塊木棒加固,木板的長為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com