
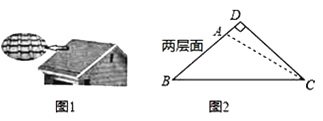
【題目】太陽能光伏建筑是現代綠色環保建筑之一,老張準備把自家屋頂改建成光伏瓦面,改建前屋頂截面△ABC如圖2所示,BC=10米,∠ABC=∠ACB=36°,改建后頂點D在BA的延長線上,且∠BDC=90°,求改建后南屋面邊沿增加部分AD的長.(結果精確到0.1米)
(參考數據:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
【答案】1.9米
【解析】試題分析:在直角三角形BCD中,由BC與sinB的值,利用銳角三角函數定義求出CD的長,在直角三角形ACD中,由∠ACD度數,以及CD的長,利用銳角三角函數定義求出AD的長即可.
試題解析:∵∠BDC=90°,BC=10,sinB=![]() , ∴CD=BCsinB=10×0.59=5.9,
, ∴CD=BCsinB=10×0.59=5.9,
∵在Rt△BCD中,∠BCD=90°﹣∠B=90°﹣36°=54°, ∴∠ACD=∠BCD﹣∠ACB=54°﹣36°=18°,
∴在Rt△ACD中,tan∠ACD=![]() , ∴AD=CDtan∠ACD=5.9×0.32=1.888≈1.9(米),
, ∴AD=CDtan∠ACD=5.9×0.32=1.888≈1.9(米),
則改建后南屋面邊沿增加部分AD的長約為1.9米.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:初中數學 來源: 題型:
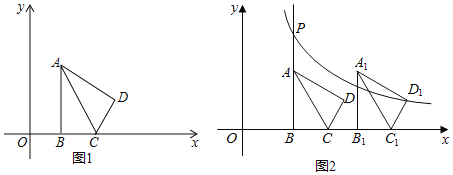
【題目】如圖1,在平面直角坐標系xOy中,已知△ABC,∠ABC=90°,頂點A在第一象限,B,C在x軸的正半軸上(C在B的右側),BC=2,AB=2![]() ,△ADC與△ABC關于AC所在的直線對稱.
,△ADC與△ABC關于AC所在的直線對稱.
(1)當OB=2時,求點D的坐標;
(2)若點A和點D在同一個反比例函數的圖象上,求OB的長;
(3)如圖2,將第(2)題中的四邊形ABCD向右平移,記平移后的四邊形為A1B1C1D1,過點D1的反比例函數y=![]() (k≠0)的圖象與BA的延長線交于點P.問:在平移過程中,是否存在這樣的k,使得以點P,A1,D為頂點的三角形是直角三角形?若存在,請直接寫出所有符合題意的k的值;若不存在,請說明理由.
(k≠0)的圖象與BA的延長線交于點P.問:在平移過程中,是否存在這樣的k,使得以點P,A1,D為頂點的三角形是直角三角形?若存在,請直接寫出所有符合題意的k的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某駐村扶貧小組實施產業扶貧,幫助貧困農戶進行西瓜種植和銷售.已知西瓜的成本為6元/千克,規定銷售單價不低于成本,又不高于成本的兩倍.經過市場調查發現,某天西瓜的銷售量y(千克)與銷售單價x(元/千克)的函數關系如下圖所示:
(1)求y與x的函數解析式(也稱關系式);
(2)求這一天銷售西瓜獲得的利潤的最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售一批名牌襯衫,平均每天可售出10件,每件盈利40元,為了擴大銷售,增加盈利,盡快減少庫存,商場決定采取適當的降價措施.經調查發現,如果每件襯衫每降價1元,商場平均每天可多售出1件,若商場平均每天要盈利600元,每件襯衫應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】交通工程學理論把在單向道路上行駛的汽車看成連續的流體,并用流量、速度、密度三個概念描述車流的基本特征,其中流量![]() (輛
(輛![]() 小時)指單位時間內通過道路指定斷面的車輛數;速度
小時)指單位時間內通過道路指定斷面的車輛數;速度![]() (千米
(千米![]() 小時)指通過道路指定斷面的車輛速度,密度
小時)指通過道路指定斷面的車輛速度,密度![]() (輛
(輛![]() 千米)指通過道路指定斷面單位長度內的車輛數.為配合大數據治堵行動,測得某路段流量
千米)指通過道路指定斷面單位長度內的車輛數.為配合大數據治堵行動,測得某路段流量![]() 與速度
與速度![]() 之間關系的部分數據如下表:
之間關系的部分數據如下表:
速度v(千米/小時) |
|
|
|
|
|
|
|
|
流量q(輛/小時) |
|
|
|
|
|
|
|
|
(1)根據上表信息,下列三個函數關系式中,刻畫![]() ,
,![]() 關系最準確是_____________________.(只填上正確答案的序號)
關系最準確是_____________________.(只填上正確答案的序號)
①![]() ;②
;②![]() ;③
;③![]()
(2)請利用(1)中選取的函數關系式分析,當該路段的車流速度為多少時,流量達到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 滿足
滿足![]() ,請結合(1)中選取的函數關系式繼續解決下列問題:市交通運行監控平臺顯示,當
,請結合(1)中選取的函數關系式繼續解決下列問題:市交通運行監控平臺顯示,當![]() 時道路出現輕度擁堵.試分析當車流密度
時道路出現輕度擁堵.試分析當車流密度![]() 在什么范圍時,該路段將出現輕度擁堵?
在什么范圍時,該路段將出現輕度擁堵?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABCD的邊長為1,E為BC邊的延長線上一點,CE=1,連接AE,與CD交于點F,連接BF并延長與線段DE交于點G,則BG的長為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
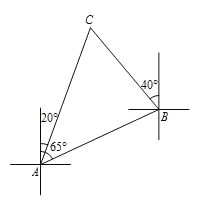
【題目】如圖,一艘船由A港沿北偏東65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏東20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏東20°方向.
求:(1)∠C的度數;
(2)A,C兩港之間的距離為多少km.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校的學生除了體育課要進行體育鍛煉外,寒暑假期間還要自己抽時間進行體育鍛煉,為了了解同學們假期體育鍛煉的情況,開學時體育老師隨機抽取了部分同學進行調查,按鍛煉的時間x(分鐘)分為以下四類:A類(![]() ),B類(
),B類(![]() ),C類(
),C類(![]() ),D類(
),D類(![]() ),對調查結果進行整理并繪制了如圖所示的不完整的折線統計圖和扇形統計圖,請結合圖中的信息解答下列各題:
),對調查結果進行整理并繪制了如圖所示的不完整的折線統計圖和扇形統計圖,請結合圖中的信息解答下列各題:
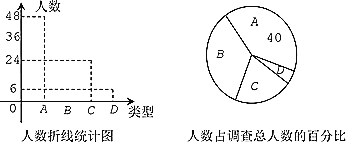
(1)扇形統計圖中D類所對應的圓心角度數為 ,并補全折線統計圖;
(2)現從A類中選出兩名男同學和三名女同學,從以上五名同學中隨機抽取兩名同學進行采訪,請利用畫樹狀圖或列表的方法求出抽到的學生恰好是一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
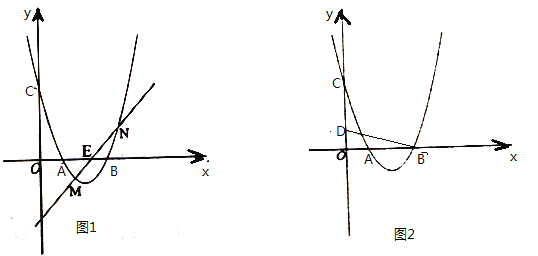
(1)填空:![]() ,
,![]() .
.
(2)如圖1,已知![]() ,過點
,過點![]() 的直線與拋物線交于點
的直線與拋物線交于點![]() 、
、![]() ,且點
,且點![]() 、
、![]() 關于點
關于點![]() 對稱,求直線
對稱,求直線![]() 的解析式.
的解析式.
(3)如圖2,已知![]() ,
,![]() 是第一象限內拋物線上一點,作
是第一象限內拋物線上一點,作![]() 軸于點
軸于點![]() ,若
,若![]() 與
與![]() 相似,請求出點
相似,請求出點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com