
【題目】在平面直角坐標(biāo)系中,二次函數(shù)y=ax2+2nx+c的圖象過坐標(biāo)原點(diǎn).
(1)若a=-1.
①當(dāng)函數(shù)自變量的取值范圍是-1≤x≤2,且n≥2時,該函數(shù)的最大值是8,求n的值;
②當(dāng)函數(shù)自變量的取值范圍是![]() 時,設(shè)函數(shù)圖象在變化過程中最高點(diǎn)的縱坐標(biāo)為m,求m與n的函數(shù)關(guān)系式,并寫出n的取值范圍;
時,設(shè)函數(shù)圖象在變化過程中最高點(diǎn)的縱坐標(biāo)為m,求m與n的函數(shù)關(guān)系式,并寫出n的取值范圍;
(2)若二次函數(shù)的圖象還過點(diǎn)A(-2,0),橫、縱坐標(biāo)都是整數(shù)的點(diǎn)叫做整點(diǎn).已知點(diǎn)![]() ,二次函數(shù)圖象與直線AB圍城的區(qū)域(不含邊界)為T,若區(qū)域T內(nèi)恰有兩個整點(diǎn),直接寫出a的取值范圍.
,二次函數(shù)圖象與直線AB圍城的區(qū)域(不含邊界)為T,若區(qū)域T內(nèi)恰有兩個整點(diǎn),直接寫出a的取值范圍.
【答案】(1) ①n=3;② 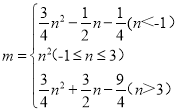 (2)
(2)![]()
【解析】
(1)①根據(jù)已知條件可確定拋物線圖象的基本特征,從而列出關(guān)于![]() 的方程,即可得解;②根據(jù)二次函數(shù)圖象的性質(zhì)分三種情況進(jìn)行分類討論,從而得到
的方程,即可得解;②根據(jù)二次函數(shù)圖象的性質(zhì)分三種情況進(jìn)行分類討論,從而得到![]() 與
與![]() 的分段函數(shù)關(guān)系;
的分段函數(shù)關(guān)系;
(2)由![]() 得正負(fù)進(jìn)行分類討論,結(jié)合已知條件求得
得正負(fù)進(jìn)行分類討論,結(jié)合已知條件求得![]() 的取值范圍.
的取值范圍.
解:(1) ∵拋物線過坐標(biāo)原點(diǎn)
∴c=0,a=-1
∴y=-x2+2nx
∴拋物線的對稱軸為直線x=n,且n≥2,拋物線開口向下
∴當(dāng)-1≤x≤2時,y隨x的增大而增大
∴當(dāng)x=2時,函數(shù)的最大值為8
∴-4+4n=8
∴n=3.
②若![]()
則![]()
∴拋物線開口向下,在對稱軸右側(cè),![]() 隨
隨![]() 的增大而減小
的增大而減小
∴當(dāng)![]() 時,函數(shù)值最大,
時,函數(shù)值最大,![]() ;
;
若![]()
則![]()
∴此時,拋物線的頂點(diǎn)為最高點(diǎn)
∴![]() ;
;
若![]()
則![]()
∴拋物線開口向下,在對稱軸左側(cè),![]() 隨
隨![]() 的增大而增大
的增大而增大
∴當(dāng)![]() 時,函數(shù)值最大,
時,函數(shù)值最大,![]()
∴綜上所述: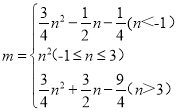
(2)結(jié)論:![]() 或
或![]()
證明:∵![]() 過
過![]()
∴![]()
∴![]()
①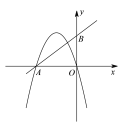
∵若![]() ,直線
,直線![]() 的解析式為
的解析式為![]() ,拋物線的對稱軸為直線
,拋物線的對稱軸為直線![]()
∴頂點(diǎn)為![]() ,對稱軸與直線
,對稱軸與直線![]() 交點(diǎn)坐標(biāo)為
交點(diǎn)坐標(biāo)為![]()
∴兩個整點(diǎn)為![]() ,
,![]()
∵不含邊界
∴![]()
∴![]()
②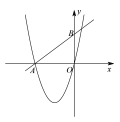
∵若![]() ,區(qū)域內(nèi)已經(jīng)確定有兩個整點(diǎn)
,區(qū)域內(nèi)已經(jīng)確定有兩個整點(diǎn)![]() ,
,![]()
∴在第三項(xiàng)象限和第一象限的區(qū)域內(nèi)都要確保沒有整點(diǎn)
∴![]()
∴![]()
∵當(dāng)![]() 時,直線上的點(diǎn)的縱坐標(biāo)為
時,直線上的點(diǎn)的縱坐標(biāo)為![]() ,拋物線上的點(diǎn)的縱坐標(biāo)為
,拋物線上的點(diǎn)的縱坐標(biāo)為![]()
∴![]()
∴![]()
∴![]()
故答案為:(1)①![]() ;②
;②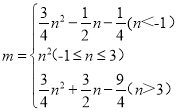 (2)
(2)![]() 或
或![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,把一個直角三角尺ACB繞著30°角的頂點(diǎn)B順時針旋轉(zhuǎn),使得點(diǎn)A與CB的延長線上的點(diǎn)E重合.
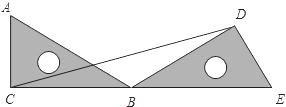
(1)三角尺旋轉(zhuǎn)了 度。
(2)連接CD,試判斷△CBD的形狀;
(3)求∠BDC的度數(shù)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形![]() 的邊長為4,延長
的邊長為4,延長![]() 至
至![]() 使
使![]() ,以
,以![]() 為邊在上方作正方形
為邊在上方作正方形![]() ,延長
,延長![]() 交
交![]() 于
于![]() ,連接
,連接![]() 、
、![]() ,
,![]() 為
為![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() 分別與
分別與![]() 、
、![]() 交于點(diǎn)
交于點(diǎn)![]() 、
、![]() .則下列結(jié)論:①
.則下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結(jié)論有( )
.其中正確的結(jié)論有( )
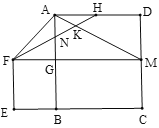
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】請你仔細(xì)觀察下面一組圖形,依據(jù)其變化規(guī)律推斷第(5)個圖形中所有正方形面積之和為____________(其中圖 中出現(xiàn)的三角形均是直角三角形,四邊形均是正方形).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC的頂點(diǎn)坐標(biāo)分別為A(0,1)、B(3,3)、C(1,3).
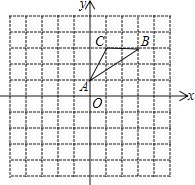
(1) 畫出△ABC關(guān)于點(diǎn)O的中心對稱圖形△A1B1C1
(2) 畫出△ABC繞原點(diǎn)O逆時針旋轉(zhuǎn)90°的△A2B2C2,直接寫出點(diǎn)C2的坐標(biāo)為______.
(3) 若△ABC內(nèi)一點(diǎn)P(m,n)繞原點(diǎn)O逆時針旋轉(zhuǎn)90°的對應(yīng)點(diǎn)為Q,則Q的坐標(biāo)為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】熊組長準(zhǔn)備為我們年級投資1萬元圍一個矩形的運(yùn)動場地(如圖),其中一邊靠墻,另外三邊選用不同材料建造且三邊的總長為![]() ,墻長
,墻長![]() ,平行于墻的邊的費(fèi)用為200元/
,平行于墻的邊的費(fèi)用為200元/![]() ,垂直于墻的邊的費(fèi)用150元/
,垂直于墻的邊的費(fèi)用150元/![]() ,設(shè)平行與墻的邊長為
,設(shè)平行與墻的邊長為![]() .
.
(1)若運(yùn)動場地面積為![]() ,求
,求![]() 的值;
的值;
(2)當(dāng)運(yùn)動場地的面積最大時是否會超了預(yù)算.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角坐標(biāo)系中,矩形![]() 的頂點(diǎn)
的頂點(diǎn)![]() 與原點(diǎn)重合,
與原點(diǎn)重合,![]() 、
、![]() 分別在坐標(biāo)軸上,
分別在坐標(biāo)軸上,![]() ,
,![]() ,直線
,直線![]() 交
交![]() ,
,![]() 分別于點(diǎn)
分別于點(diǎn)![]() ,
,![]() ,反比例函數(shù)
,反比例函數(shù)![]() 的圖象經(jīng)過點(diǎn)
的圖象經(jīng)過點(diǎn)![]() ,
,![]() .
.
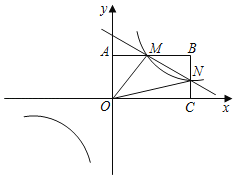
(1)求反比例函數(shù)的解析式;
(2)直接寫出當(dāng)![]() 時,
時,![]() 的取值范圍;
的取值范圍;
(3)若點(diǎn)![]() 在
在![]() 軸上,且
軸上,且![]() 的面積與四邊形
的面積與四邊形![]() 的面積相等,求點(diǎn)
的面積相等,求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方形ABCD中,AD=4![]() ,把邊CD繞點(diǎn)C逆時針旋轉(zhuǎn)30度得到線段CE,連接BE并延長,交AD于點(diǎn)F,連接DE,則線段EF的長度為________
,把邊CD繞點(diǎn)C逆時針旋轉(zhuǎn)30度得到線段CE,連接BE并延長,交AD于點(diǎn)F,連接DE,則線段EF的長度為________

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 的
的![]() 與
與![]() 的部分對應(yīng)值如下表:
的部分對應(yīng)值如下表:
| -1 | 0 | 1 | 3 |
| -3 | 1 | 3 | 1 |
下列結(jié)論:①拋物線的開口向下;②其圖象的對稱軸為![]() ;③當(dāng)
;③當(dāng)![]() 時,函數(shù)值
時,函數(shù)值![]() 隨
隨![]() 的增大而增大;④方程
的增大而增大;④方程![]() 有一個根大于4.其中正確的結(jié)論有( )
有一個根大于4.其中正確的結(jié)論有( )
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com