
【題目】如圖①,AB是⊙O的直徑,![]() ,連接AC.
,連接AC.
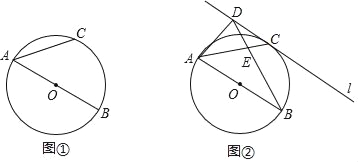
(1)求證:∠CAB=45°;
(2)如圖②,直線l經過點C,在直線l上取一點D,使BD=AB,BD與AC相交于點E,連接AD,且AD=AE.
①求證:直線l是⊙O的切線;
②求![]() 的值.
的值.
【答案】(1)證明見解析(2)①證明見解析②![]()
【解析】
(1)連接BC,由![]() 知∠CAB=∠ABC,根據AB為⊙O的直徑得∠ACB=90°,據此可得答案;(2)①連接OC、作DP⊥AB,設∠ABD=α,先根據AD=AE、BA=BD求得∠ABD=∠DAE=30°,據此知PD=
知∠CAB=∠ABC,根據AB為⊙O的直徑得∠ACB=90°,據此可得答案;(2)①連接OC、作DP⊥AB,設∠ABD=α,先根據AD=AE、BA=BD求得∠ABD=∠DAE=30°,據此知PD=![]() BD=
BD=![]() AB,結合OC=
AB,結合OC=![]() AB知DP=OC,據此證得四邊形DPOC為矩形,繼而得證;②證△ACD∽△BAE得
AB知DP=OC,據此證得四邊形DPOC為矩形,繼而得證;②證△ACD∽△BAE得![]() =
=![]() =
=![]() ,據此知AE=
,據此知AE=![]() CD,作EI⊥AB于點I,由∠CAB=45°、∠ABD=30°知BE=2EI=2×
CD,作EI⊥AB于點I,由∠CAB=45°、∠ABD=30°知BE=2EI=2×![]() AE=
AE=![]() AE=2CD,據此可得答案.
AE=2CD,據此可得答案.
(1)如圖①,連接BC,
∵![]() ,
,
∴∠CAB=∠ABC,
∵AB為⊙O的直徑,
∴∠ACB=90°,
∴∠CAB=∠CBA=45°;
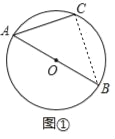
(2)①如圖②,連接OC、作DP⊥AB于點P,
設∠ABD=α,
∵BA=BD,
∴∠BAD=∠BDA,
∵AD=AE,
∴∠ADE=∠AED,
∴∠AED=∠BAD,
∴∠DAE=∠DBA=α,
∵∠CAB=45°,
∴∠ADE=∠AED=∠CAB+∠ABD=45°+α,
∵∠DAE+∠ADE+∠AED=180°,
∴α+α+45°+α+45°=180°,
解得:α=30°,即∠ABD=∠DAE=30°,
在Rt△BPD中,PD=![]() BD=
BD=![]() AB,
AB,
又∵OC=![]() AB,
AB,
∴OC=PD,
∵△ABC是等腰直角三角形,OA=OB,
∴CO⊥AB,
∵DP⊥AB、CO⊥AB,
∴四邊形DPOC是矩形,
∴∠OCD=90°,
∴直線l是⊙O的切線;
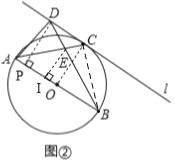
②由①知,∠CAD=∠ABE=30°,CD∥AB,
∴∠ACD=∠EAB=45°,
則△ACD∽△BAE,
∴![]() =
=![]() =
=![]() ,
,
∴AE=![]() CD,
CD,
如圖②,作EI⊥AB于點I,
∵∠CAB=45°、∠ABD=30°,
∴BE=2EI=2×![]() AE=
AE=![]() AE=
AE=![]() ×
×![]() CD=2CD,
CD=2CD,
∴![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
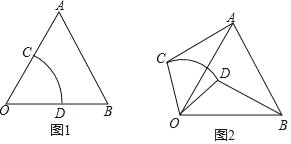
【題目】在等邊△AOB中,將扇形COD按圖1擺放,使扇形的半徑OC、OD分別與OA、OB重合,OA=OB=2,OC=OD=1,固定等邊△AOB不動,讓扇形COD繞點O逆時針旋轉,線段AC、BD也隨之變化,設旋轉角為α.(0<α≤360°)
(1)當OC∥AB時,旋轉角α= 度;
發現:(2)線段AC與BD有何數量關系,請僅就圖2給出證明.
應用:(3)當A、C、D三點共線時,求BD的長.
拓展:(4)P是線段AB上任意一點,在扇形COD的旋轉過程中,請直接寫出線段PC的最大值與最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,四邊形ABCD中,E是對角線AC上一點,DE=EC,以AE為直徑的⊙O與邊CD相切于點D,點B在⊙O上,連接OB.
(1)求證:DE=OE;
(2)若CD∥AB,求證:BC是⊙O的切線;
(3)在(2)的條件下,求證:四邊形ABCD是菱形.
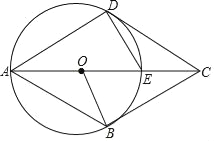
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=![]() x2﹣x﹣
x2﹣x﹣![]() .
.
(1)在平面直角坐標系內,畫出該二次函數的圖象;
(2)根據圖象寫出:①當x 時,y>0;
②當0<x<4時,y的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的部分圖象如圖所示,圖象過點(﹣1,0),對稱軸為直線x=2,下列結論:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若點A(﹣3,y1)、點B(﹣![]() ,y2)、點C(
,y2)、點C(![]() ,y3)在該函數圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結論有( )
,y3)在該函數圖象上,則y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結論有( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OABC是邊長為1的正方形,OC與x軸正半軸的夾角為15°,點B在拋物線y=ax2(a<0)的圖象上,則a的值為( )
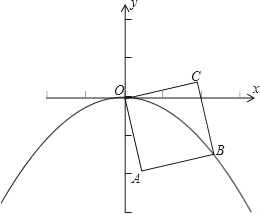
A. ![]() B.
B. ![]() C. ﹣2 D.
C. ﹣2 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,二次函數y=ax2﹣2ax﹣3a(a<0)的圖象與x軸交于A、B兩點(點A在點B的右側),與y軸的正半軸交于點C,頂點為D.
(1)求頂點D的坐標(用含a的代數式表示);
(2)若以AD為直徑的圓經過點C.
①求拋物線的函數關系式;
②如圖2,點E是y軸負半軸上一點,連接BE,將△OBE繞平面內某一點旋轉180°,得到△PMN(點P、M、N分別和點O、B、E對應),并且點M、N都在拋物線上,作MF⊥x軸于點F,若線段MF:BF=1:2,求點M、N的坐標;
③點Q在拋物線的對稱軸上,以Q為圓心的圓過A、B兩點,并且和直線CD相切,如圖3,求點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小梅家的陽臺上放置了一個曬衣架如圖1,圖2是曬衣架的側面示意圖,A,B兩點立于地面,將曬衣架穩固張開,測得張角∠AOB=62°,立桿OA=OB=140cm,小梅的連衣裙穿在衣架后的總長度為122cm,問將這件連衣裙垂掛在曬衣架上是否會拖落到地面?請通過計算說明理由(參考數據:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
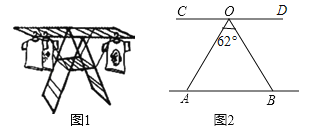
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABO為底角是30°的等腰三角形,OA=AB=4,O為坐標原點,點B在x軸上,點P在直線AB上運動,當線段OP最短時,點P的坐標為( )
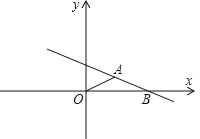
A. (1,1) B. (![]() ,3) C. (3,
,3) C. (3,![]() ) D. (2,2)
) D. (2,2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com