
【題目】某電子廠生產一種新型電子產品,每件制造成本為20元,試銷過程中發現,每月銷售量y(萬件)與銷售單價x(元)之間的關系可以近似地看作一次函數y=﹣2x+100.(利潤=售價﹣制造成本)
(1)寫出每月的利潤z(萬元)與銷售單價x(元)之間的函數關系式;
(2)當銷售單價為多少元時,廠商每月獲得的利潤為400萬元?
(3)根據相關部門規定,這種電子產品的銷售單價不能高于40元,如果廠商每月的制造成本不超過520萬元,那么當銷售單價為多少元時,廠商每月獲得的利潤最大?最大利潤為多少萬元?
【答案】(1)z=﹣2x2+140x﹣2000;(2)30元或40元;(3)當銷售單價為37元時,廠商每月獲得的利潤最大,最大利潤為442萬元.
【解析】試題分析:(1)根據每月的利潤z=(x-18)y,再把y=-2x+100代入即可求出z與x之間的函數解析式,
(2)把z=440代入z=-2x2+136x-1800,解這個方程即可;
(3)根據廠商每月的制造成本不超過520萬元,以及成本價20元,得出銷售單價的取值范圍,進而得出最大利潤.
試題解析:(1)z=(x﹣20)y=(x﹣20)(﹣2x+100)=﹣2x2+140x﹣2000,
故z與x之間的函數解析式為z=﹣2x2+140x﹣2000;
(2)由z=400,得400=﹣2x2+140x﹣2000,
解這個方程得x1=30,x2=40
所以銷售單價定為30元或40元;
(3)∵廠商每月的制造成本不超過520萬元,每件制造成本為20元,
∴每月的生產量小于等于![]() =26萬件,
=26萬件,
由y=﹣2x+100≤26,得:x≥37,
又由限價40元,得37≤x≤40,
∵z=﹣2x2+140x﹣2000=﹣2(x﹣35)2+450,
∴圖象開口向下,對稱軸右側z隨x的增大而減小,
∴當x=37時,z最大為442萬元.
當銷售單價為37元時,廠商每月獲得的利潤最大,
最大利潤為442萬元.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:
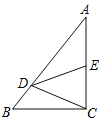
【題目】如圖,在Rt△ABC中,∠C=90°,點D在邊AB上,線段DC繞點D逆時針旋轉,端點C恰巧落在邊AC上的點E處.如果![]() ,
,![]()
求m與n滿足的關系式(用含n的代數式表示m).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD的面積為300cm2,長和寬的比為3:2.在此長方形內沿著邊的方向能否并排裁出兩個面積均為147cm2的圓(π取3),請通過計算說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市舉行“行動起來,對抗霧霾”為主題的植樹活動,某街道積極響應,決定對該街道進行綠化改造,共購進甲、乙兩種樹共50棵,已知甲樹每棵800元,乙樹每棵1200元.
(1)若購買兩種樹的總金額為56000元,求甲、乙兩種樹各購買了多少棵?
(2)若購買甲樹的金額不少于購買乙樹的金額,至少應購買甲樹多少棵?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊 ABC 的邊長是 2 , D 、 E 分別為 AB 、 AC 的中點,連接CD ,過 E 點作 EF // DC 交 BC 的延長線于點 F
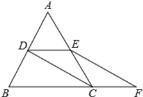
(1) 求證:四邊形 CDEF 是平行四邊形;
(2)求四邊形 CDEF 的周長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級春游,現有36座和42座兩種客車供選擇租用,若只租用36座客車若干輛,則正好坐滿;若只租用42座客車,則能少租一輛,且有一輛車沒有坐滿,但超過30人;已知36座客車每輛租金400元,42座客車每輛租金440元.
(1)該校七年級共有多少人參加春游?
(2)請你幫該校設計一種最省錢的租車方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
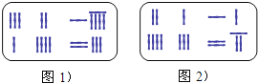
【題目】《九章算術》是我國東漢初年編訂的一部數學經典著作.在它的“方程”一章里,一次方程組是由算籌布置而成的.《九章算術》中的算籌圖是豎排的,為看圖方便,我們把它改為橫排,如圖1、圖2.圖中各行從左到右列出的算籌數分別表示未知數x,y的系數與相應的常數項.把圖1所示的算籌圖用我們現在所熟悉的方程組形式表述出來,就是![]() ,類似地,圖2所示的算籌圖我們可以表述為( )
,類似地,圖2所示的算籌圖我們可以表述為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠B =∠C,點D、E分別是邊AB、AC上的點,PD平分∠BDE交BC于H,PE平分∠DEC交BC于G,DQ平分∠ADE交PE延長線于Q。

(1)∠A+∠B+∠C+∠P +∠Q = °;
(2)猜想∠P與∠A的數量關系,并證明你的猜想;
(3)若∠EGH =112°,求∠ADQ 的大小。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com