
【題目】小明在課外研究中,設計如下題目:直線![]() 過點
過點![]() ,
,![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于點
交于點![]() .
.
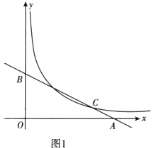
(1)求直線和曲線的關系式.(圖1)
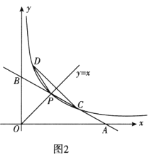
(2)小明發現曲線![]() 關于直線
關于直線![]() 對稱,他把曲線
對稱,他把曲線![]() 與直線
與直線![]() 的交點
的交點![]() 叫做曲線的頂點.(圖2)
叫做曲線的頂點.(圖2)
①直接寫出![]() 點的坐標;
點的坐標;
②若點![]() 從
從![]() 點出發向上運動,運動到
點出發向上運動,運動到![]() 時停止,求此時
時停止,求此時![]() 的面積.
的面積.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,②
,②![]() .
.
【解析】
(1)把![]() ,
,![]() 代入
代入![]() ,列出關于k和b的二元一次方程組,求出k和b的值,即可求出直線
,列出關于k和b的二元一次方程組,求出k和b的值,即可求出直線![]() 的解析式,把點
的解析式,把點![]() 代入直線解析式,求出n=1,把
代入直線解析式,求出n=1,把 ![]() 代入
代入![]() ,即可求出曲線的解析式.
,即可求出曲線的解析式.
(2)列方程組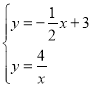 ,方程組的解,即為P點的坐標,由曲線
,方程組的解,即為P點的坐標,由曲線![]() 關于直線
關于直線![]() 對稱,
對稱,![]() ,可得點C和點D 關于
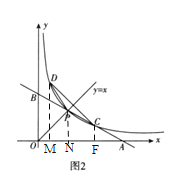
,可得點C和點D 關于![]() 對稱,解點D的坐標,通過做輔助線,分別過點D、點P、點C向x軸作垂線,分別交x軸于點M、點N、點F,得到
對稱,解點D的坐標,通過做輔助線,分別過點D、點P、點C向x軸作垂線,分別交x軸于點M、點N、點F,得到![]() ,求得
,求得![]() 的面積.
的面積.
(1)將點![]() ,
,![]() 的坐標代入
的坐標代入![]() ,
,
得:![]() ,解得
,解得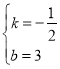
∴直線解析式為:![]() ,
,
∵直線![]() 過點
過點![]()
∴把C點坐標代入![]() 得,n=1,
得,n=1,
∴C點坐標為![]() ,
,
將C點坐標代入![]() ,解得m=4,
,解得m=4,
∴曲線的關系式為:![]() .
.
(2) ①∵點P是曲線![]() 與直線
與直線![]() 的交點,
的交點,
∴得到方程組![]() ,解得,
,解得,![]() 或
或![]() ,
,
∵x>0,
∴P點的坐標為![]()
②分別過點D、點P、點C向x軸作垂線,分別交x軸于點M、點N、點F.
∵曲線![]() 關于直線
關于直線![]() 對稱,
對稱,
∴當![]() 時,點C和點D 關于
時,點C和點D 關于![]() 對稱,
對稱,
∴點D得坐標為(1,4),
∴![]()
![]() ,
,
∴![]() .
.


 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:初中數學 來源: 題型:
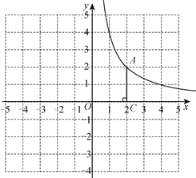
【題目】如圖,在平面直角坐標系xOy中,函數![]() 的圖象經過點
的圖象經過點![]() ,作AC⊥x軸于點C.
,作AC⊥x軸于點C.
(1)求k的值;
(2)直線AB:![]() 圖象經過點
圖象經過點![]() 交x軸于點
交x軸于點![]() .橫、縱坐標都是整數的點叫做整點.線段AB,AC,BC圍成的區域(不含邊界)為W.
.橫、縱坐標都是整數的點叫做整點.線段AB,AC,BC圍成的區域(不含邊界)為W.
①直線AB經過![]() 時,直接寫出區域W內的整點個數;
時,直接寫出區域W內的整點個數;
②若區域W內恰有1個整點,結合函數圖象,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年10月18日,黨的十九大報告提出“鄉村振興”戰略,之后各地發展鄉村旅游,某村在2018年3月1日首次舉辦“百花節”,開園免費賞花,于是大批游客涌入該村賞花,吃農家飯買土特產,平均每人消費100元.
(1)據統計,某個周六早上開園后平均每小時有500人進園,兩小時后,平均每小時有100人離園,園區規定,當園區內游客人數達到3000時,將停止進園,那么從開園起經過多少小時后停止進園?
(2)該村對園區加大建設和宣傳力度,2019年3月1日,第二屆“百花節”如期開園,同時規定進園門票費為每人60元,受各種因素影響,與2018年同期相比,人數在20000的基礎上降低了a%,除門票外平均每人消費金額增長了![]() a%,園區總收入增長了
a%,園區總收入增長了![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
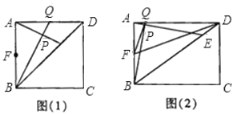
【題目】在四邊形ABCD中,點E是對角線BD上一點,點Q是AD邊上一點,BQ交AE于點P,∠ABQ=∠DAE,點F是AB邊的中點.
(1)當四邊形ABCD是正方形時,如圖(1).
①若BE=BA,求證:△ABP≌△EBP;
②若BE=4DE,求證:AF2=AQ·AD.
(2)當四邊形ABCD是矩形時,如圖(2),連接FQ,FD.若BE=4DE,求證:∠AFQ=∠ADF.
查看答案和解析>>
科目:初中數學 來源: 題型:
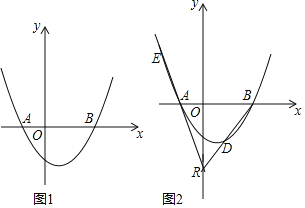
【題目】已知拋物線y=a(x2-cx-2c2)(a>0)交x軸于A、B兩點(點A在點B的左側),交y軸于點C.
(1) 取A(-1,0),則點B的坐標為___________;
(2) 若A(-1,0),a=1,點P為第一象限的拋物線,以P為圓心,![]() 為半徑的圓恰好與AC相切,求P點坐標;
為半徑的圓恰好與AC相切,求P點坐標;
(3) 如圖,點R(0,n)在y軸負半軸上,直線RB交拋物線于另一點D,直線RA交拋物線于E.若DR=DB,EF⊥y軸于F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數 y=ax2+bx+c(a≠0)的圖象如圖所示,對稱軸是直線 x=1,下列結論:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0. 其中正確的是( )
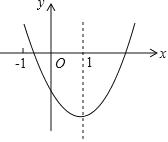
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 分別交y軸、x軸于A、B兩點,拋物線y=﹣x2+bx+c過A、B兩點.
分別交y軸、x軸于A、B兩點,拋物線y=﹣x2+bx+c過A、B兩點.
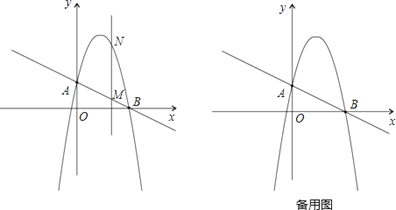
(1)求這個拋物線的解析式;
(2)作垂直x軸的直線x=t,在第一象限交直線AB于M,交這個拋物線于N.求當t取何值時,MN有最大值?最大值是多少?
(3)在(2)的情況下,以A、M、N、D為頂點作平行四邊形,求第四個頂點D的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com