
【題目】如圖,拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸相交于點
軸相交于點![]() ,且點
,且點![]() 與點
與點![]() 的坐標分別為
的坐標分別為![]() .
.![]() ,點
,點![]() 是拋物線的頂點.點
是拋物線的頂點.點![]() 為線段
為線段![]() 上一個動點,過點
上一個動點,過點![]() 作
作![]() 軸于點
軸于點![]() ,若
,若![]() .
.
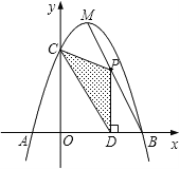
(1)求二次函數解析式;
(2)設![]() 的面積為
的面積為![]() ,試判斷
,試判斷![]() 有最大值或最小值?若有,求出其最值,若沒有,請說明理由;
有最大值或最小值?若有,求出其最值,若沒有,請說明理由;
(3)在![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為直角三角形?若存在,請寫出點
為直角三角形?若存在,請寫出點![]() 的坐標若不存在,請說明理由.
的坐標若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)將點B,C的坐標代入y=-x2+bx+c即可;
(2)把(1)中的一般式配成頂點式可得到M(1,4),設直線BM的解析式為y=kx+n,再利用待定系數法求出直線BM的解析式,則P(m,-2m+6)(1≤m<3),于是根據三角形面積公式得到S=-m2+3m,然后根據二次函數的性質即可解決問題;
(3)討論:∠PDC不可能為90°;當∠DPC=90°時,易得-2m+6=3,解方程求出m即可得到此時P點坐標;當∠PCD=90°時,利用勾股定理得到和兩點間的距離公式得到m2+(-2m+3)2+32+m2=(-2m+6)2,然后解方程求出滿足條件的m的值即可得到此時P點坐標.
解:(1)把![]() ,
,![]() 代入
代入![]() ,
,
得![]()
解得![]()
∴拋物線解析式為:![]() ;
;
(2)∵![]() ,
,
∴頂點![]() ,
,
∵![]() ,
,
∴設![]() 的解析式為:
的解析式為:![]()
![]()
則有![]()
解得![]() ,
,
∴![]() 的解析式為:
的解析式為:![]() ,
,
∵![]() ,
,![]() 軸
軸
∴![]() ,則
,則![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]()
∴![]() 有最大值,
有最大值,
當![]() 時,
時,![]() ;
;
(3)存在,
①![]() 時,如圖①
時,如圖①
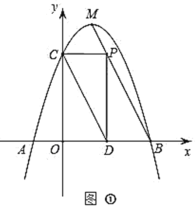
∵![]() 軸
軸
∴![]() 時,
時,![]() 軸
軸
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴此時![]() ;
;
②![]() 時,如圖②,
時,如圖②,
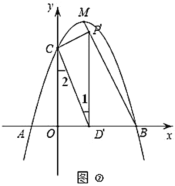
∵![]() 軸,
軸,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
![]() ,
,
∴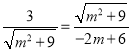 ,
,
∴![]() ,
,
![]() ,
,
解得:![]() (舍),
(舍),![]() ,
,
∴![]() ;
;
③∵![]() 軸,
軸,![]() 在
在![]() 軸的正半軸上,
軸的正半軸上,
∴![]() 不可能等于
不可能等于![]() ;
;
綜上所述,![]() 或
或![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:
【題目】受“新冠”疫情影響,全國中小學延遲開學,很多學校都開展起了“線上教學”,市場上對手寫板的需求激增.重慶某廠家準備3月份緊急生產A,B兩種型號的手寫板,若生產20個A型號和30個B型號手寫板,共需要投入36000元;若生產30個A型號和20個B型號手寫板,共需要投入34000元.
(1)請問生產A,B兩種型號手寫板,每個各需要投入多少元的成本?
(2)經測算,生產的A型號手寫板每個可獲利200元,B型號手寫板每個可獲利400元,該廠家準備用10萬元資金全部生產這兩種手寫板,總獲利w元,設生產了A型號手寫板a個,求w關于a的函數關系式;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D,E分別在△ABC的邊BC,AC上,連接AD,DE.
(1)若∠C=∠BAD,AB=5,求BD·BC的值;
(2)若點E是AC的中點,AD=![]() AE, 求證:∠1=∠C.
AE, 求證:∠1=∠C.
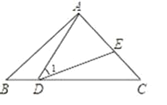
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學計劃購進若干個甲種規格的排球和乙種規格的足球. 如果購買20個甲種規格的排球和15個乙種規格的足球,一共需要花費2050元; 如果購買10個甲種規格的排球和20個乙種規格的足球,一共需要花費1900元.
(1)求每個甲種規格的排球和每個乙種規格的足球的價格分別是多少元?
(2)如果學校要購買甲種規格的排球和乙種規格的足球共50個,并且預算總費用不超過3210元,那么該學校至多能購買多少個乙種規格的足球?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某漁船在海面上朝正西方向以20海里/時勻速航行,在A處觀測到燈塔C在北偏西60°方向上,航行1小時到達B處,此時觀察到燈塔C在北偏西30°方向上,若該船繼續向西航行至離燈塔距離最近的位置,求此時漁船到燈塔的距離(結果精確到1海里,參考數據: ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,D是![]() 的中點,BC與AD,OD分別交于點E,F.
的中點,BC與AD,OD分別交于點E,F.
(1)求證:OD∥AC;
(2)求證:DC2=DEDA;
(3)若⊙O的直徑AB=10,AC=6,求BF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把矩形紙片ABCD沿EF折疊,使點B落在邊AD上的點B'處,點A落在點A'處.
(1)求證:B'E=BF;
(2)若AE=1,B'E=2,求梯形ABFE的面積.
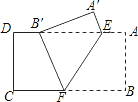
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某小區居民使用共享單車次數的情況,某研究小組隨機采訪該小區的10位居民,得到這10位居民一周內使用共享單車的次數統計如下:
使用次數 | 0 | 5 | 10 | 15 | 20 |
人數 | 1 | 1 | 4 | 3 | 1 |
(1)這10位居民一周內使用共享單車次數的中位數是 次,眾數是 次.
(2)若小明同學把數據“20”看成了“30”,那么中位數,眾數和平均數中不受影響的是 .(填“中位數”,“眾數”或“平均數”)
(3)若該小區有2000名居民,試估計該小區居民一周內使用共享單車的總次數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).
(1) 請畫出△ABC向左平移5個單位長度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 請畫出△ABC關于原點對稱的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.
軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com