【題目】為弘揚中華優秀傳統文化，今年2月20日舉行了襄陽市首屆中小學生經典誦讀大賽決賽. 某中學為了選拔優秀學生參加，廣泛開展校級“經典誦讀”比賽活動，比賽成績評定為A，B，C，D，E五個等級，該校七(1)班全體學生參加了學校的比賽，并將比賽結果繪制成如下兩幅不完整的統計圖．請根據圖中信息，解答下列問題：
(1)該校七(1)班共有 名學生；扇形統計圖中C等級所對應扇形的圓心角等于 度；
(2)補全條形統計圖；
(3)若A等級的4名學生中有2名男生2名女生，現從中任意選取2名參加學校培訓班，請用列表法或畫樹狀圖的方法，求出恰好選到1名男生和1名女生的概率．
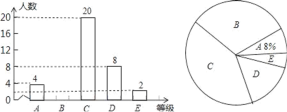
【答案】（1）50，144°；（2）補圖見解析；（3）
【解析】試題分析：（1）由A的人數和其所占的百分比即可求出總人數；C的人數可知，而總人數已求出，進而可求出其所對應扇形的圓心角的度數；
（2）根據求出的數據即可補全條形統計圖；
（3）列表得出所有等可能的情況數，找出剛好抽到一男一女的情況數，即可求出所求的概率．
試題解析：（1）由題意可知總人數=4÷8%=50人；扇形統計圖中C等級所對應扇形的圓心角=20÷50×100%×360°=144°；
（2）補全條形統計圖如圖所示：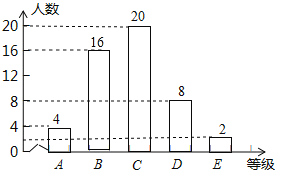
（3）列表如為
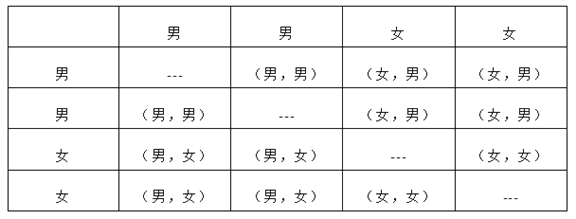
由上表可知，從4名學生中任意選取2名學生共有12種等可能結果，其中恰好選到1名男生和1名女生的結果有8種.
所以，恰好選到1名男生和1名女生的概率P=
=
.
黃岡天天練口算題卡系列答案科目：初中數學 來源： 題型：
【題目】如圖，函數y=
（x＜0）的圖象與直線y=
x+m相交于點A和點B．過點A作AE⊥x軸于點E，過點B作BF⊥y軸于點F，P為線段AB上的一點，連接PE、PF．若△PAE和△PBF的面積相等，且xP=﹣
，xA﹣xB=﹣3，則k的值是（ ）
A. ﹣5 B. 
C. ﹣2 D. ﹣1
查看答案和解析>>
科目：初中數學 來源： 題型：
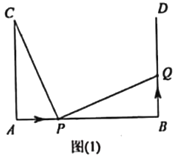
【題目】如圖(1)
，
，BD⊥AB，
，點
在線段
上以
的速度由點
向點
運動，同時，點
在線段
上由點向點
運動，它們運動的時間為
.
(1)若點的速度與點的速度相等，當
時，求證：
；
(2)在(1)的條件下，判斷此時
和
的位置關系，并證明；
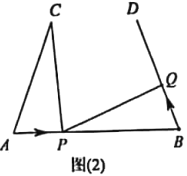
(3)將圖(1)中的“，
”，改為“
”，得到圖(2)，其他條件不變.設點的運動速度為
，請問是否存在實數
，使得
與
全等？若存在，求出相應的和
的值；若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2013年6月，某中學結合廣西中小學閱讀素養評估活動，以“我最喜愛的書籍”為主題，對學生最喜愛的一種書籍類型進行隨機抽樣調查，收集整理數據后，繪制出以下兩幅未完成的統計圖，請根據圖1和圖2提供的信息，解答下列問題：
（1）在這次抽樣調查中，一共調查了多少名學生？
（2）請把折線統計圖（圖1）補充完整；
（3）求出扇形統計圖（圖2）中，體育部分所對應的圓心角的度數；
（4）如果這所中學共有學生1800名，那么請你估計最喜愛科普類書籍的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，點A、B、C、D是坐標軸上的點且點C坐標是（0，﹣1），AB=5，點（a，b）在如圖所示的陰影部分內部（不包括邊界），已知OA=OD=4，則a的取值范圍是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：矩形ABCD中，AB＝4，BC＝3，點M、N分別在邊AB、CD上，直線MN交矩形對角線 AC于點E，將△AME沿直線MN翻折，點A落在點P處，且點P在射線CB上.
(1)如圖1，當EP⊥BC時，求CN的長；
(2) 如圖2，當EP⊥AC時，求AM的長；
(3) 請寫出線段CP的長的取值范圍，及當CP的長最大時MN的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為保護環境，我市公交公司計劃購買A型和B型兩種環保節能公交車共10輛．若購買A型公交車1輛，B型公交車2輛，共需400萬元；若購買A型公交車2輛，B型公交車1輛，共需350萬元．
（1）求購買A型和B型公交車每輛各需多少萬元？
（2）預計在某線路上A型和B型公交車每輛年均載客量分別為60萬人次和100萬人次．若該公司購買A型和B型公交車的總費用不超過1200萬元，且確保這10輛公交車在該線路的年均載客總和不少于680萬人次，則該公司有哪幾種購車方案？
（3）在（2）的條件下，哪種購車方案總費用最少？最少總費用是多少萬元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x一元二次方程x2-2(k+1)x+k2-2k-3=0有兩個不相等的實數根
（1）求k取值范圍；
（2）當k最小的整數時，求拋物線 y= x2-2(k+1)x+k2-2k-3的頂點坐標以及它與x軸的交點坐標；
（3）將（2）中求得的拋物線在x軸下方的部分沿x軸翻折到x軸上方，圖象的其余部分不變，得到一個新圖象．請你畫出這個新圖象，并求出新圖象與直線 y=x+m有三個不同公共點時m值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y=-x+1和直線y=x-2相交于點P，分別與y軸交于A、B兩點．
（1）求點P的坐標；
（2）求△ABP的面積；
（3）M、N分別是直線y=-x+1和y=x-2上的兩個動點，且MN∥y軸，若MN=5，直接寫出M、N兩點的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com