
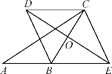
【題目】已知:如圖,在△ABC中,O是邊BC的中點,E是線段AB延長線上一點,過點C作CD∥BE,交線段EO的延長線于點D,連接BD,CE.
(1)求證:CD=BE;
(2)如果∠ABD=2∠BED,求證:四邊形BECD是菱形.
【答案】見解析
【解析】
(1)可通過全等三角形來證明簡單的線段相等,△COD和△BOE中,已知了CO=BO,∠COD=∠BOE,CD∥BE,因此不難得出兩三角形全等,進而可得出CD=BE.
(2)需先證明四邊形AFCE是平行四邊形,那么鄰邊相等的平行四邊形是菱形.
(1)∵CD∥BE,
∴∠CDE=∠DEB.
∵O是邊BC的中點,
∴CO=BO.
在△COD和△BOE中,

∴△COD≌△BOE(AAS).
∴CD=BE.
(2)∵CD∥BE,CD=BE,
∴四邊形BECD是平行四邊形.
∵∠ABD=2∠BED,∠ABD=∠BED+∠BDE,
∴∠BED=∠BDE.
∴BD=BE.
∴四邊形BECD是菱形.


科目:初中數學 來源: 題型:
【題目】如圖,OC是∠AOB內的一條射線,OD、OE分別平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,則∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),則∠BOC= °,∠DOE= °;
(3)猜想:∠DOE與∠BOC有怎樣的數量關系?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,OM是∠AOC的角平分線,ON是∠BOC的角平分線.
(1)當∠AOB=90°,∠BOC=40°時,求∠MON的度數.
(2)若∠AOB的度數不變,∠BOC的度數為α時,求∠MON的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=BC=4,AO=BO,P是射線CO上的一個動點,∠AOC=60°,則當△PAB為直角三角形時,AP的長為 __________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中(AD>AB),點E是BC上一點,且DE=DA,AF⊥DE,垂足為點F,在下列結論中,不一定正確的是( )

A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與x軸、y軸分別交于點A和點B,點C、D分別為線段AB、OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為( )
與x軸、y軸分別交于點A和點B,點C、D分別為線段AB、OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為( )

A.(﹣3,0) B.(﹣6,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知圖①中拋物線y=ax2+bx+c經過點D(﹣1,0)、C(0,﹣1)、E(1,0).
(1)求圖①中拋物線的函數表達式; 
(2)將圖①中拋物線向上平移一個單位,再繞原點O順時針旋轉180°后得到圖②中拋物線,則圖②中拋物線的函數表達式為; 
(3)圖②中拋物線與直線y=﹣ ![]() x﹣
x﹣ ![]() 相交于A、B兩點(點A在點B的左側),如圖③,求點A、B的坐標,并直接寫出當一次函數的值大于二次函數的值時,x的取值范圍.
相交于A、B兩點(點A在點B的左側),如圖③,求點A、B的坐標,并直接寫出當一次函數的值大于二次函數的值時,x的取值范圍. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校實施課程改革,為初三學生設置了A,B,C,D,E,F共六門不同的拓展性課程,現隨機抽取若干學生進行了“我最想選的一門課”調查,并將調查結果繪制成如圖統計圖表(不完整)
選修課 | A | B | C | D | E | F |
人數 | 20 | 30 |
根據圖標提供的信息,下列結論錯誤的是( )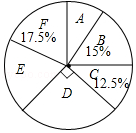
A.這次被調查的學生人數為200人
B.扇形統計圖中E部分扇形的圓心角為72°
C.被調查的學生中最想選F的人數為35人
D.被調查的學生中最想選D的有55人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E是BC的中點,連接AE并延長交DC的延長線于點F.

(1)求證:AB=CF;
(2)連接DE,若AD=2AB,求證:DE⊥AF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com