
【題目】如圖,菱形紙片![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 邊的中點(diǎn),折疊紙片,使點(diǎn)
邊的中點(diǎn),折疊紙片,使點(diǎn)![]() 落在直線
落在直線![]() 上的
上的![]() 處,折痕為經(jīng)過(guò)點(diǎn)
處,折痕為經(jīng)過(guò)點(diǎn)![]() 的線段
的線段![]() .則
.則![]() 的度數(shù)為________.
的度數(shù)為________.
【答案】75°
【解析】
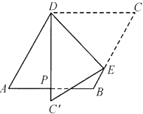
連接BD,可知△ABD是等邊三角形,根據(jù)三線合一的性質(zhì)得出DP平分∠ADB,即∠ADP=30°,再根據(jù)折疊性質(zhì)可知,∠PDE=∠CDE=75°,然后根據(jù)三角形的內(nèi)角和定理求出答案.
解:連接BD,
∵菱形![]() 中,
中,![]() ,
,
∴AD=AB,AB∥CD
∴△ABD是等邊三角形,∠ADC=120°
∵PA=PB
∴∠ADP=∠BDP=30°
根據(jù)折疊的性質(zhì)可知:∠PDE=∠CDE
∴∠CDE=(∠ADC-∠ADP) ÷2=(120°-30°)÷2=45°
∵∠CDE+∠C+![]() =180°
=180°
∴![]() =180°-(∠CDE+∠C)=180°-(45°+60°)=75°
=180°-(∠CDE+∠C)=180°-(45°+60°)=75°
故答案為:75°



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
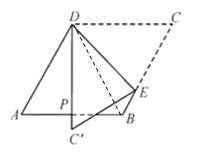
【題目】如圖,正方形網(wǎng)格中每個(gè)小正方形邊長(zhǎng)都是1.
(1)畫(huà)出△ABC關(guān)于直線1對(duì)稱的圖形△A1BlCl;
(2)在直線l上找一點(diǎn)P,使PB=PC;(要求在直線1上標(biāo)出點(diǎn)P的位置)
(3)連接PA、PC,計(jì)算四邊形PABC的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() ,垂足為
,垂足為![]() ,連接
,連接![]() .
.

(1)如圖1,![]() 與
與![]() 的數(shù)量關(guān)系是__________.
的數(shù)量關(guān)系是__________.
(2)如圖2,若![]() 是線段
是線段![]() 上一動(dòng)點(diǎn)(點(diǎn)
上一動(dòng)點(diǎn)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 、
、![]() 重合),連接
重合),連接![]() ,將線段
,將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() 得到線段
得到線段![]() ,連接
,連接![]() ,請(qǐng)猜想
,請(qǐng)猜想![]() 三者之間的數(shù)量關(guān)系,并證明你的結(jié)論;
三者之間的數(shù)量關(guān)系,并證明你的結(jié)論;
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
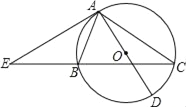
【題目】如圖,△ABC內(nèi)接于⊙O,AD是⊙O直徑,過(guò)點(diǎn)A的切線與CB的延長(zhǎng)線交于點(diǎn)E.
(1)求證:EA2=EBEC;
(2)若EA=AC,cos∠EAB=![]() ,AE=12,求⊙O的半徑.
,AE=12,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
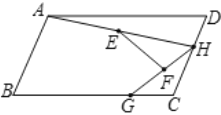
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的動(dòng)點(diǎn).連接
上的動(dòng)點(diǎn).連接![]() 、
、![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 為
為![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() .則
.則![]() 的最大值與最小值的差為( )
的最大值與最小值的差為( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某汽車(chē)銷(xiāo)售公司4月份銷(xiāo)售某廠汽車(chē),在一定范圍內(nèi),每輛汽車(chē)的進(jìn)價(jià)與銷(xiāo)售量有如下關(guān)系:若當(dāng)月僅售出1輛汽車(chē),則該汽車(chē)的進(jìn)價(jià)為30萬(wàn)元,每多售出1輛,所有售出汽車(chē)的進(jìn)價(jià)均降低0.1萬(wàn)元/輛,月底廠家一次性返利給銷(xiāo)售公司,每輛返利0.5萬(wàn)元.
(1)若該公司當(dāng)月售出5輛汽車(chē),則每輛汽車(chē)的進(jìn)價(jià)為 萬(wàn)元.
(2)若汽車(chē)的售價(jià)為31萬(wàn)/輛,該公司計(jì)劃當(dāng)月盈利12萬(wàn)元,那么需要售出多少輛汽車(chē)?(盈利=銷(xiāo)售利潤(rùn)+返利)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系中,反比例函數(shù)y=![]() (x>0),過(guò)點(diǎn)A(3,4).
(x>0),過(guò)點(diǎn)A(3,4).
(1)求y關(guān)于x的函數(shù)表達(dá)式.
(2)求當(dāng)y≥2時(shí),自變量x的取值范圍.
(3)在x軸上有一點(diǎn)P(1,0),在反比例函數(shù)圖象上有一個(gè)動(dòng)點(diǎn)Q,以PQ為一邊作一個(gè)正方形PQRS,當(dāng)正方形PQRS有兩個(gè)頂點(diǎn)在坐標(biāo)軸上時(shí),畫(huà)出狀態(tài)圖并求出相應(yīng)S點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小亮想了解一根彈簧的長(zhǎng)度是如何隨所掛物體質(zhì)量的變化而變化的,他把這根彈簧的上端固定,在其下端懸掛物體.下面是小亮測(cè)得的彈簧的長(zhǎng)度y與所掛物體質(zhì)量x的幾組對(duì)應(yīng)值.
所掛質(zhì)量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
彈簧長(zhǎng)度y/cm | 30 | 32 | 34 | 36 | 38 | 40 |
(1)上表所反映的變化過(guò)程中的兩個(gè)變量,________是自變量,________是因變量;
(2)直接寫(xiě)y與x的關(guān)系式;
(3)當(dāng)彈簧長(zhǎng)度為130cm(在彈簧承受范圍內(nèi))時(shí),求所掛重物的質(zhì)量.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖一,在平面直角坐標(biāo)系中,![]() 是
是![]() 軸正半軸上一點(diǎn),
軸正半軸上一點(diǎn),![]() 是第四象限一點(diǎn),
是第四象限一點(diǎn),![]() 軸,交
軸,交![]() 軸負(fù)半軸于
軸負(fù)半軸于![]() ,且(a-2)+|b+3|=0,
,且(a-2)+|b+3|=0,![]() 四邊形AOBC=12.
四邊形AOBC=12.
(1)求![]() 點(diǎn)坐標(biāo)
點(diǎn)坐標(biāo)
(2)如圖二,設(shè)![]() 為線段
為線段![]() 上一動(dòng)點(diǎn)(點(diǎn)
上一動(dòng)點(diǎn)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合),求證:∠ADB+∠DBC-∠OAD=180°
重合),求證:∠ADB+∠DBC-∠OAD=180°
(3)如圖三,當(dāng)![]() 點(diǎn)在線段
點(diǎn)在線段![]() 上運(yùn)動(dòng)(點(diǎn)
上運(yùn)動(dòng)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合),
重合),![]() 點(diǎn)在線段
點(diǎn)在線段![]() 上運(yùn)動(dòng)(點(diǎn)
上運(yùn)動(dòng)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合)時(shí),連接
重合)時(shí),連接![]() 、
、![]() 作∠OAD、∠DEB的平分線交于
作∠OAD、∠DEB的平分線交于![]() 點(diǎn),請(qǐng)你探索∠AFE與∠ADE之間的關(guān)系,并說(shuō)明理由.
點(diǎn),請(qǐng)你探索∠AFE與∠ADE之間的關(guān)系,并說(shuō)明理由.

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com