
【題目】如圖,點O為平面直角坐標系的原點,在長方形OABC中,OC∥AB,OA∥BC,兩邊OC、OA分別在x軸和y軸上,且點B(a,b)滿足:![]() +(2b+6)2=0.
+(2b+6)2=0.
(1)求點B的坐標;
(2)如圖1,若過點B的直線BP與長方形OABC的邊交于點P,且將長方形OABC的面積分為1:3兩部分,求點P的坐標;
(3)如圖2,M為線段OC一點,且∠ABM=∠AMB,N是x軸負半軸上一動點,∠MAN的平分線AD交BM的延長線于點D,在點N運動的過程中,試判斷∠ANM與∠D的數量關系,并說明理由.

【答案】(1)B(4,﹣3)(2)(2,0)或(0,﹣![]() )(3)∠ANM=2∠D
)(3)∠ANM=2∠D
【解析】
(1)利用非負數的性質即可解決問題;
(2)分兩種情形分別討論求解即可;
(3)結論:∠ANM=2∠D.作ME∥AD交AB于E.延長BA到F.利用平行線的性質,角平分線的定義即可解決問題;
(1)由題意:4﹣a=0,2b+6=0,
∴a=4,b=﹣3,
∴B(4,﹣3).
(2)①當點P在OC上時,由題意:S△BCP:S四邊形OABC=1:4,
∴![]() CP3=
CP3=![]() ×3×4,
×3×4,
∴PC=2.
∴OP=4﹣2=2,
∴P(2,0).
②當點P中OA上時,S△ABP=![]() S四邊形OABC,
S四邊形OABC,
∴![]() PA4=
PA4=![]() ×3×4
×3×4
∴PA=![]() ,
,
∴OP=3﹣![]() =
=![]() ,
,
∴P(0,﹣![]() ),
),
綜上所述,滿足條件的點P坐標為(2,0)或(0,﹣![]() ).
).
(3)結論:∠ANM=2∠D.
理由:作ME∥AD交AB于E.延長BA到F.
∵ME∥AD,
∴∠1=∠D,∠2=∠3,
∵AD平分∠MAN,
∴∠MAN=2∠3,
∵OC∥AB,
∴∠ABM=∠CMB,
∵∠AMB=∠CMB,
∴∠AMC=2∠AMB,
∵OC∥AB,
∴∠FAM=∠AMC=2∠AMB,
∴∠ANM=2∠AMB﹣2∠3
=2∠AMB﹣2∠2
=2(∠AMB﹣∠2)
=2∠1
=2∠D.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】拋物線![]() 經過點A(
經過點A(![]() ,0),B(
,0),B(![]() ,0),且與y軸相交于點C.
,0),且與y軸相交于點C.
(1)求這條拋物線的表達式;
(2)求∠ACB的度數;
(3)設點D是所求拋物線第一象限上一點,且在對稱軸的右側,點E在線段AC上,且DE⊥AC,當△DCE與△AOC相似時,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P為定角∠AOB的平分線上的一個定點,且∠MPN與∠AOB互補.若∠MPN在繞點P旋轉的過程中,其兩邊分別與OA,OB相交于M、N兩點,則以下結論:(1)PM=PN恒成立,(2)OM+ON的值不變,(3)四邊形PMON的面積不變,(4)MN的長不變,
其中正確的為__________(請填寫結論前面的序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學課上,張老師出示了一個題目:“如圖,ABCD的對角線相交于點O,過點O作EF垂直于BD交AB,CD分別于點F,E,連接DF,BE.請根據上述條件,寫出一個正確結論.”其中四位同學寫出的結論如下:
小青:OE=OF;小何:四邊形DFBE是正方形;
小夏:S四邊形AFED=S四邊形FBCE;小雨:∠ACE=∠CAF.
這四位同學寫出的結論中不正確的是( )

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】證明命題“對角線相等的平行四邊形是矩形”,要根據題意,畫出圖形,并用符號表示已知和求證,寫出證明過程,下面是小張同學根據題意畫出的圖形,并寫出了不完整的已知和求證.
已知:如圖,ABCD是平行四邊形,AC與BD是對角線,且 .
求證: .
請你補全已知和求證,并寫出證明過程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AC上取點B,在其同一側作兩個等邊三角形△ABD 和△BCE ,連接AE,CD與GF,下列結論正確的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,輪船從A港出發,以28海里/小時的速度向正北方向航行,此時測的燈塔M在北偏東30°的方向上.半小時后,輪船到達B處,此時測得燈塔M在北偏東60°的方向上.
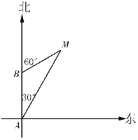
(1)求輪船在B處時與燈塔M的距離;
(2)輪船從B處繼續沿正北方向航行,又經半小時后到達C處.求:此時輪船與燈塔M的距離是多少?燈塔M在輪船的什么方向上?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一個可以自由轉動的轉盤中,指針位置固定,三個扇形的面積都相等,且分別標有數字1,2,3.

(1)小明轉動轉盤一次,當轉盤停止轉動時,指針所指扇形中的數字是奇數的概率為________;
(2)小明先轉動轉盤一次,當轉盤停止轉動時,記錄下指針所指扇形中的數字;接著再轉動轉盤一次,當轉盤停止轉動時,再次記錄下指針所指扇形中的數字,求這兩個數字之和是3的倍數的概率(用畫樹狀圖或列表等方法求解)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com