
【題目】如圖,利用我們現(xiàn)在已經(jīng)學(xué)過的圓和銳角三角函數(shù)的知識可知,半徑 r 和圓心角θ及其所對的弦長 l之間的關(guān)系為![]() ,從而
,從而![]()
![]() ,綜合上述材料當(dāng)
,綜合上述材料當(dāng)![]() 時,
時,![]() ______.
______.

科目:初中數(shù)學(xué) 來源: 題型:
【題目】被歷代數(shù)學(xué)家尊為“算經(jīng)之首”的《九章算術(shù)》是中國古代算法的扛鼎之作.《九章算術(shù)》中記載:“今有五雀、六燕,集稱之衡,雀俱重,燕俱輕.一雀一燕交而處,衡適平.并燕、雀重一斤.問燕、雀一枚各重幾何?”
譯文:“今有![]() 只雀、
只雀、![]() 只燕,分別聚焦而且用衡器稱之,聚在一起的雀重,燕輕.經(jīng)一只雀、一只燕交換位置而放,重量相等.
只燕,分別聚焦而且用衡器稱之,聚在一起的雀重,燕輕.經(jīng)一只雀、一只燕交換位置而放,重量相等.![]() 只雀、
只雀、![]() 只燕重量為
只燕重量為![]() 斤.問雀、燕每
斤.問雀、燕每![]() 只各重多少斤?”
只各重多少斤?”
請列方程組解答上面的問題.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,若二次函數(shù)![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() (-1,0)、
(-1,0)、![]() ,與
,與![]() 軸交于點
軸交于點![]() (0,4),連接
(0,4),連接![]() 、
、![]() ,且拋物線的對稱軸為直線
,且拋物線的對稱軸為直線![]() .
.
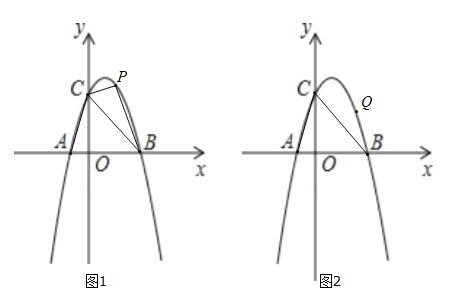
(1)求二次函數(shù)的解析式;
(2)若點![]() 是拋物線在一象限內(nèi)
是拋物線在一象限內(nèi)![]() 上方一動點,且點
上方一動點,且點![]() 在對稱軸的右側(cè),連接
在對稱軸的右側(cè),連接![]() 、
、![]() ,是否存在點
,是否存在點![]() ,使
,使![]() ?若存在,求出點
?若存在,求出點![]() 的坐標(biāo);若不存在,說明理由;
的坐標(biāo);若不存在,說明理由;
(3)如圖2,若點![]() 是拋物線上一動點,且滿足
是拋物線上一動點,且滿足![]() ,請直接寫出點
,請直接寫出點![]() 坐標(biāo).
坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
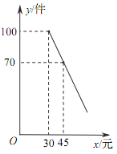
【題目】某商店購進(jìn)一批成本為每件 30 元的商品,經(jīng)調(diào)查發(fā)現(xiàn),該商品每天的銷售量 y(件)與銷售單價 x(元)之間滿足一次函數(shù)關(guān)系,其圖象如圖所示.
(1)求該商品每天的銷售量 y 與銷售單價 x 之間的函數(shù)關(guān)系式;
(2)若商店按單價不低于成本價,且不高于 50 元銷售,則銷售單價定為多少,才能使銷售該商品每天獲得的利潤 w(元)最大?最大利潤是多少?
(3)若商店要使銷售該商品每天獲得的利潤不低于 800 元,則每天的銷售量最少應(yīng)為多少件?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,CD 為⊙O 的直徑,弦 AB 交 CD 于點E,連接 BD、OB.

(1)求證:△AEC∽△DEB;
(2)若 CD⊥AB,AB=6,DE=1,求⊙O 的半徑長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某交為了開展“陽光體育運(yùn)動”,計劃購買籃球和足球,已知足球的單價比籃球的單價多![]() 元.若購買
元.若購買![]() 個籃球和
個籃球和![]() 個足球需花費
個足球需花費![]() 元.
元.
(1)求籃球和足球的單價各是多少元;
(2)若學(xué)校購買籃球和足球共![]() 個,且購買籃球的總金額不超過購買足球的總金額,則學(xué)校最多可購買多少個籃球?
個,且購買籃球的總金額不超過購買足球的總金額,則學(xué)校最多可購買多少個籃球?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
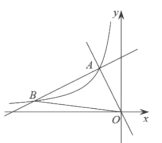
【題目】如圖,在平面直角坐標(biāo)系![]() 中,一次函數(shù)
中,一次函數(shù)![]() 和
和![]() 的圖象相交于點
的圖象相交于點![]() ,反比例函數(shù)
,反比例函數(shù)![]() 的圖象經(jīng)過點
的圖象經(jīng)過點![]() .
.
(1)求反比例函數(shù)的表達(dá)式;
(2)設(shè)一次函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象的另一個交點為
的圖象的另一個交點為![]() ,連接
,連接![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,AC=BC,∠ACB=90°,點D,E分別在AC,BC上,且CD=CE.
(1)如圖1,求證:∠CAE=∠CBD;
(2)如圖2,F(xiàn)是BD的中點,求證:AE⊥CF;
(3)如圖3,F(xiàn),G分別是BD,AE的中點,若AC=2![]() ,CE=1,求△CGF的面積.
,CE=1,求△CGF的面積.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com