
【題目】如圖,已知CD是△ABC中AB邊上的高,以CD為直徑的⊙O分別交CA、CB于點E、F,點G是AD的中點.
(1)求證:GE是⊙O的切線;
(2)當△ADC滿足怎樣的條件時,四邊形EGDO恰為正方形?(直接寫出結果即可)

【答案】(1)見解析;(2)當△ADC滿足∠A=45°時,四邊形EGDO恰為正方形.
【解析】
(1)連接OE、DE,如圖,利用圓周角定理得到∠CED=90°,再根據斜邊上的中線性質得GE=GA=GD,則∠GED=∠GDE,加上∠OED=∠ODE,所以∠GEO=90°,然后根據切線的判定定理得到結論;
(2)當∠DOE=90°時易得四邊形EGDO正方形,此時△OCE為等腰直角三角形,于是可判斷當△ADC滿足∠A=45°時,四邊形EGDO恰為正方形.
(1)證明:連接OE、DE,如圖,
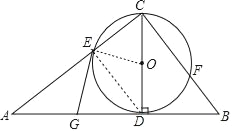
∵CD為直徑,
∴∠CED=90°,
∵G點AD的中點,
∴GE=GA=GD,
∴∠GED=∠GDE,
而OD=OE,
∴∠OED=∠ODE,
∴∠GEO=∠GDC,
而CD為高,
∴∠GDC=90°,
∴∠GEO=90°,
∴OE⊥GE,
∴GE是⊙O的切線;
(2)當∠DOE=90°時,四邊形EGDO為矩形,而OE=OD,則四邊形EGDO正方形,
此時△OCE為等腰直角三角形,
所以當△ADC滿足∠A=45°時,四邊形EGDO恰為正方形.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
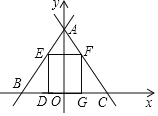
【題目】如圖,直線y=kx+b與直線y=2x+6關于y軸對稱且交于點A,直線y=2x+6交x軸于點B,直線y=kx+b交x軸于點C,正方形DEFG一邊DG在線段BC上,點E在線段AB上,點F在線段AC上,則點G的坐標是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】)如圖,在△ABC中,D是BC邊上的中點,F、E分別是AD及其延長線上的點,CF∥BE。

(1)試說明△BDE≌△CDF
(2)請連接BF、CE,試判斷四邊形BECF是何種特殊四邊形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列各式及其驗證過程:![]() ,驗證:
,驗證:![]() .
.![]() , 驗證:
, 驗證:![]() .
.
(1)按照上述兩個等式及其驗證過程,猜想![]() 的變形結果并進行驗證.
的變形結果并進行驗證.
(2)針對上述各式反映的規律,寫出用a(a為任意自然數,且a≥2)表示的等式,并給出驗證.
(3)針對三次根式及n次根式(n為任意自然數,且n≥2),有無上述類似的變形?如果有,寫出用a(a為任意自然數,且a≥2)表示的等式,并給出驗證.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小林準備進行如下操作實驗:把一根長為![]() 的鐵絲剪成兩段,并把每一段各圍成一個正方形.
的鐵絲剪成兩段,并把每一段各圍成一個正方形.
![]() 要使這兩個正方形的面積之和等于
要使這兩個正方形的面積之和等于![]() ,小林該怎么剪?
,小林該怎么剪?
![]() 小峰對小林說:“這兩個正方形的面積之和不可能等于
小峰對小林說:“這兩個正方形的面積之和不可能等于![]() .”他的說法對嗎?請說明理由.
.”他的說法對嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
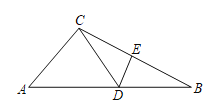
【題目】如圖,△ABC中,D為AB上一點,E為BC上一點,且AC=CD=BD=BE=2.
(1)若∠A=40°,求∠CDE;
(2)若圖形中所有線段長均為整數,求CE.
查看答案和解析>>
科目:初中數學 來源: 題型:
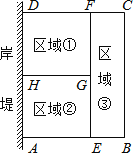
【題目】為了節省材料,小浪底水庫養殖戶小李利用水庫的岸堤(足夠長)為一邊,用總長為120米的網在水庫中圍成了如圖所示的①②③三塊矩形區域,而且這三塊矩形區域的面積相等.設BC的長度為xm,矩形區域ABCD的面積為ym2.
(1)求y與x之間的函數關系式,并注明自變量x的取值范圍;
(2)請你幫養殖戶小李計算一下BC邊多長時,養殖區ABCD面積最大,最大面積為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明和小亮利用三張卡片做游戲,卡片上分別寫有A,B,B.這些卡片除字母外完全相同,從中隨機摸出一張,記下字母后放回,充分洗勻后,再從中摸出一張,如果兩次摸到卡片字母相同則小明勝,否則小亮勝,這個游戲對雙方公平嗎?請說明現由.
查看答案和解析>>
科目:初中數學 來源: 題型:
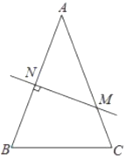
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 的垂直平分線交
的垂直平分線交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)若![]() ,則
,則![]() 的度數是 ;
的度數是 ;
(2)連接![]() ,若
,若![]() ,
,![]() 的周長是
的周長是![]() .
.
①求![]() 的長;
的長;
②在直線![]() 上是否存在點
上是否存在點![]() ,使由
,使由![]() ,
,![]() ,
,![]() 構成的
構成的![]() 的周長值最小?若存在,標出點
的周長值最小?若存在,標出點![]() 的位置并求
的位置并求![]() 的周長最小值;若不存在,說明理由.
的周長最小值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com