
【題目】已知:如圖,△ABC與△ADE,AB=AC,AD=AE,且∠BAC=∠DAE=40°,CD與BE相交于點F,連接AF則下列結論:①CD=BE:②△ABF≌△ACF;③∠BFD=140°;④FA平分∠BFD;⑤∠FAC=∠FAE.其中正確的結論有( )

A.2個B.3個C.4個D.5個
【答案】A
【解析】
根據已知條件易證△ABE≌△ACD,得到BE=CD即可判斷①,根據兩條邊相等無法判斷△ABF≌△ACF,根據已知條件不能得到∠BFC=40°,故可判斷③,作AM⊥BE,AN⊥CD,根據全等三角形的性質得到AM=AN,可得AF平分∠BFD,故可判斷④⑤.
∵∠BAC=∠DAE=40°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠CAD,又AB=AC,AD=AE
∴△ABE≌△ACD
∴BE=CD,①正確;
∵AB=AC,AF=FA,∠BAF≠∠CAF,
∴△ABF與△ACF不全等,故②錯誤;
∴∠BAC≠∠BFC=40°,則∠BFD≠140°,③錯誤;
作AM⊥BE,AN⊥CD,∵△ABE≌△ACD
∴AM=AN,
∴AF平分∠BFD,AF不平分∠CAE,故④正確,⑤錯誤,
故選A.



科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,邊AB、AC的垂直平分線分別交BC于E、F,若∠EAF=90°,AF=3,AE=4.
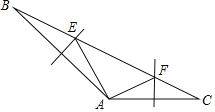
(1)求邊BC的長;(2)求出∠BAC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 某校七年級共有男生63名,為了參加全校運動會,七年級準備從本年級所有男生中挑選出身高相差不多的40名男生組成儀仗隊,為此,收集到所有男生的身高數據(單位:cm),經過整理獲得如下信息:
a.小明把所有男生的身高數據按由低到高整理為如下,但因為不小心有部分數據被墨跡遮擋:

b.小剛繪制了七年級所有男生身高的頻數分布表
身高分組 | 劃記 | 頻數 |
149≤x<152 | 丅 | 2 |
152≤x<155 | 正一 | 6 |
155≤x<158 | 正正丅 | 12 |
158≤x<161 | 正正正 | 19 |
161≤x<164 | 正正 | 10 |
164≤x<167 | ______ | ______ |
167≤x<170 | ______ | ______ |
170≤x<173 | 丅 | 2 |
c.該校七年級男生身高的平均數、中位數、眾數如下:
平均數 | 中位數 | 眾數 |
160 | m | n |
根據以上信息,回答下列問題:
(1)補全b表中頻數分布表;
(2)直接寫出c表中m,n的值;
(3)借助于已給信息,確定挑選出參加儀仗隊的男生的身高范圍;
(4)若本區七年級共有男生1260名,利用以上數據估計,全區七年級男生身高達到160及以上的男生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC的角平分線與BC的垂直平分線交與點D,DE⊥AB,DF⊥AC,垂足分別為E,F.若AB=10,AC=8.
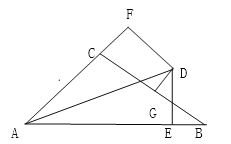
(1)求證:CF=BE;
(2) 求BE長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察如圖所示的一組圖形,其中圖形①中共有2顆星,圖形②中共有6顆星,圖形③中共有11顆星,圖形④中共有17顆星,…,按此規律,圖形⑧中星星的顆數是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)己知:如圖,△ABC,∠C=90°,現將斜邊AB繞A點順時針旋轉90°到AD,過D點作DE⊥CA,交CA的延長線于點E.求證:△ABC ≌ △DAE
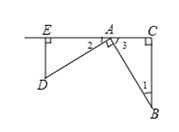
(2)如圖,四邊形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,則四邊形ABCD的面積為 。
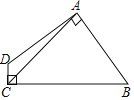
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填寫下表
序號 |
| 1 | 2 | … |
① |
| 5 |
| … |
② |
| 2 |
| … |
③ |
|
| 4 | … |
隨著![]() 值的逐漸變大,回答下列問題
值的逐漸變大,回答下列問題
(1)當![]() 時,這三個代數式中 的值最小;
時,這三個代數式中 的值最小;
(2)你預計代數式的值最先超過1000的是代數式 ,此時![]() 的值為 .
的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是工人師傅用同一種材料制成的金屬框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周長為24cm,CF=3cm,則制成整個金屬框架所需這種材料的總長度為 ________cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
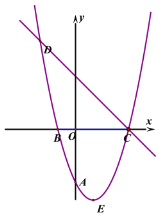
【題目】已知拋物線![]() 經過A(0,-3),B(-1,0),且拋物線對稱軸為直線
經過A(0,-3),B(-1,0),且拋物線對稱軸為直線![]() ,E
,E
是拋物線的頂點。
(1)求拋物線的解析式以及頂點坐標E。
(2)在![]() 軸上是否存在點P,使得
軸上是否存在點P,使得![]() 周長最短,若存在,請求出P點坐標,若不存在,請說
周長最短,若存在,請求出P點坐標,若不存在,請說
明理由。
(3)直線![]() 與拋物線交于C、D兩點,Q是直線DC下方拋物線上的一點,是否存在點Q
與拋物線交于C、D兩點,Q是直線DC下方拋物線上的一點,是否存在點Q
使得![]() 的面積最大,若存在請求出最大面積,若不存在,請說明理由。
的面積最大,若存在請求出最大面積,若不存在,請說明理由。
(4)拋物線上是否存在點M,使得![]() 是直角三角形,若存在,直接寫出M點坐標,若不
是直角三角形,若存在,直接寫出M點坐標,若不
存在,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com