
【題目】已知:x為實數,[x]表示不超過x的最大整數,如[3.14]=3,[1]=1,[﹣1.2]=﹣2.請你在學習,理解上述定義的基礎上,解決下列問題:設函數y=x﹣[x].
(1)當x=2.15時,求y=x﹣[x]的值;
(2)當0<x<2時,求函數y=x﹣[x]的表達式,并畫出函數圖象;
(3)當﹣2<x<2時,平面直角坐標系xOy中,以O為圓心,r為半徑作圓,且r≤2,該圓與函數y=x﹣[x]恰有一個公共點,請直接寫出r的取值范圍.
【答案】(1)0.15;(2)①y=x,②當1y=x﹣1, (3)r的取值范圍是:0<r<![]() 或x=
或x=![]() .
.
【解析】試題分析:(1)根據[x]的定義進行計算即可;
(2)由已知條件:0<x<1,1≤x<2進行分類討論,由此可求出結論;
(3)把自變題x在-2<x<2內分四種情況得出相應的函數關系式,并畫出圖形,確定r的取值即可.
試題解析:解:(1)當x=2.15時,y=x﹣[x]=2.15﹣[2.15]=2.15﹣2=0.15;
(2)①當0<x<1時,[x]=0.∵y=x﹣[x],∴y=x;
②當1≤x<2時,[x]=1
∵y=x﹣[x],∴y=x﹣1;

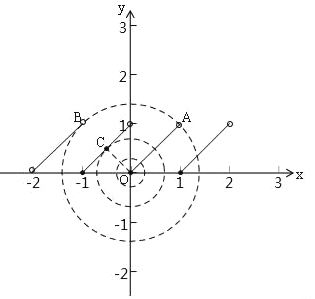
(3)函數y=x﹣[x](﹣2<x<2),如圖,OA=![]() .
.
①當﹣2<x<﹣1,[x]=﹣2,y=x﹣[x]=x+2,②當﹣1≤x<0時,[x]=﹣1,y=x﹣[x]=x+1,③當0≤x<1時,[x]=0,y=x﹣[x ]=x,④當1≤x<2時,[x]=1,y=x﹣[x]=x﹣1,當r=OA= ![]() 時,⊙O與直線y=x﹣1相交于一點,OC=
時,⊙O與直線y=x﹣1相交于一點,OC= ![]() OA=
OA=![]() ,當0<r<
,當0<r<![]() 時,⊙O總與直線y=x相交于一點;
時,⊙O總與直線y=x相交于一點;
綜上所述:r的取值范圍是:0<r<![]() 或x=
或x= ![]() .
.


科目:初中數學 來源: 題型:
【題目】(1)圖(1)是一個長為2m,寬為2n的矩形,把此矩形沿圖中虛線用剪刀均分為四個小長方形,然后按圖(2)的形狀拼成一個大正方形.請問:這兩個圖形的什么量不變?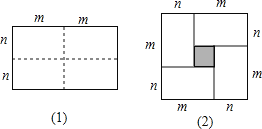
(2)把所得的大正方形面積比原矩形的面積多出的陰影部分的面積用含m,n的代數式表示為(m-n)2或m2-2mn+n2 .
(3)由前面的探索可得出的結論是:在周長一定的矩形中,當 時,面積最大.
(4)若矩形的周長為24cm,則當邊長為多少時,該圖形的面積最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
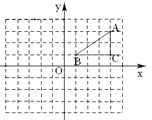
【題目】如圖,網格中的每個小正方形的邊長均為1個單位長度,Rt△ABC的頂點均在格點上,建立平面直角坐標系后,點A(4,3),點B(1,1),點C(4,1).
(1)畫出Rt△ABC關于y軸對稱的Rt△A1B1C1,(點A、B、C的對稱點分別是A1、B1、C1),直接寫出A1的坐標;
(2)將Rt△ABC向下平移4個單位,得到Rt△A2B2C2(點A、B、C的對應點分別是A2、B2、C2),畫出Rt△A2B2C2 ,連接A1C2,直接寫出線段A1C2的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
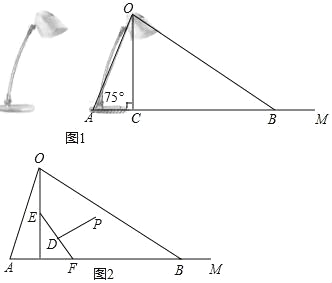
【題目】如圖1為放置在水平桌面上的臺燈的平面示意圖,燈臂AO長為50cm,與水平桌面所形成的夾角∠OAM為75°.由光源O射出的邊緣光線OC,OB與水平桌面所形成的夾角∠OCA,∠OBA分別為90°和30°.(不考慮其他因素,結果精確到0.1cm. sin75°≈0.97,cos75°≈0.26,![]() ≈1.73
≈1.73
(1)求該臺燈照亮水平桌面的寬度BC.
(2)人在此臺燈下看書,將其側面抽象成如圖2所示的幾何圖形,若書與水平桌面的夾角∠EFC為60°,書的長度EF為24cm,點P為眼睛所在位置,當點P在EF 的垂直平分線上,且到EF距離約為34cm(人的正確看書姿勢是眼睛離書距離約1尺≈34cm)時,稱點P為“最佳視點”.請通過計算說明最佳視點P在不在燈光照射范圍內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在我國南宋數學家楊輝(約13世紀)所著的《詳解九章算術》(1261年)一書中,用下圖的三角形解釋二項和的乘方規律.楊輝在注釋中提到,在他之前北宋數學家賈憲(1050年左右)也用過上述方法,因此我們稱這個三角形為“楊輝三角”或“賈憲三角”.楊輝三角兩腰上的數都是![]() ,其余每一個數為它上方(左右)兩數的和.事實上,這個三角形給出了
,其余每一個數為它上方(左右)兩數的和.事實上,這個三角形給出了![]()
![]() 的展開式(按
的展開式(按![]() 的次數由大到小的順序)的系數規律.例如,此三角形中第三行的
的次數由大到小的順序)的系數規律.例如,此三角形中第三行的![]() 個數
個數![]() ,恰好對應著
,恰好對應著![]() 展開式中的各項系數,第四行的
展開式中的各項系數,第四行的![]() 個數
個數![]() ,恰好對應著
,恰好對應著![]() 展開式中的各項系數,等等.請依據上面介紹的數學知識,解決下列問題:
展開式中的各項系數,等等.請依據上面介紹的數學知識,解決下列問題:
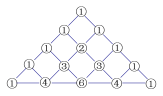
(1)寫出![]() 的展開式;
的展開式;
(2)利用整式的乘法驗證你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某銷售公司5月份銷售某種型號汽車,當月該型號汽車的進價為30萬元/輛,若當月銷售量超過5輛時,每多售出1輛,所有售出的汽車進價均降低0.1萬元/輛.根據市場調查,月銷售量不會突破30臺.
(1)設當月該型號汽車的銷售量為x輛(x≤30,且x為正整數),實際進價為y萬元/輛,當0<x≤5時,y= ; 當5<x≤30時,y= ;(直接填最后結果)
(2)已知該型號汽車的銷售價為32萬元/輛,公司計劃當月銷售利潤25萬元,那么月需售出多少輛汽車?(注:銷售利潤=銷售價﹣進價)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣![]() x+3與x軸相交于點B,與y軸相交于點A,點E為線段AB中點,∠ABO的平分線BD與y軸相較于點D,點A、C關于點O對稱.
x+3與x軸相交于點B,與y軸相交于點A,點E為線段AB中點,∠ABO的平分線BD與y軸相較于點D,點A、C關于點O對稱.
(1)求線段DE的長;
(2)一個動點P從點D出發,沿適當的路徑運動到直線BC上的點F,再沿射線CB方向移動2![]() 個單位到點G,最后從點G沿適當的路徑運動到點E處,當P的運動路徑最短時,求此時點G的坐標;
個單位到點G,最后從點G沿適當的路徑運動到點E處,當P的運動路徑最短時,求此時點G的坐標;
(3)將△ADE繞點A順時針方向旋轉,旋轉角度α(0<α≤180°),在旋轉過程中DE所在的直線分別與直線BC、直線AC相交于點M、點N,是否存在某一時刻使△CMN為等腰三角形,若存在,請求出CM的長,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,![]() ,
,![]() .點G,E分別在邊AB,CD上,點F,H在對角線AC上.若四邊形EFGH是菱形,則AG的長是( )
.點G,E分別在邊AB,CD上,點F,H在對角線AC上.若四邊形EFGH是菱形,則AG的長是( )

A.![]() B.5C.
B.5C.![]() D.6
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店購進甲、乙兩種商品,已知每件甲種商品的價格比每件乙種商品的價格貴10元,用350元購買甲種商品的件數恰好與用300元購買乙種商品的件數相同.
(1)求甲、乙兩種商品每件的價格各是多少元?
(2)計劃購買這兩種商品共50件,且投入的經費不超過3200元,那么,最多可購買多少件甲種商品?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com