
【題目】如圖,在Rt△ABC中,∠B=90°,∠A=30°,以點A為圓心,BC長為半徑畫弧交AB于點D,分別以點A、D為圓心,AB長為半徑畫弧,兩弧交于點E,連接AE,DE,則∠EAD的余弦值是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:如圖所示:設BC=x,
∵在Rt△ABC中,∠B=90°,∠A=30°,
∴AC=2BC=2x,AB= ![]() BC=
BC= ![]() x,
x,
根據題意得:AD=BC=x,AE=DE=AB= ![]() x,
x,
作EM⊥AD于M,則AM= ![]() AD=
AD= ![]() x,
x,
在Rt△AEM中,cos∠EAD= ![]() =
= ![]() =
= ![]() ;
;
故選:B.
本題考查了解直角三角形、含30°角的直角三角形的性質、等腰三角形的性質、三角函數;通過作輔助線求出AM是解決問題的關鍵.設BC=x,由含30°角的直角三角形的性質得出AC=2BC=2x,求出AB= ![]() BC=
BC= ![]() x,根據題意得出AD=BC=x,AE=DE=AB=
x,根據題意得出AD=BC=x,AE=DE=AB= ![]() x,作EM⊥AD于M,由等腰三角形的性質得出AM=
x,作EM⊥AD于M,由等腰三角形的性質得出AM= ![]() AD=
AD= ![]() x,在Rt△AEM中,由三角函數的定義即可得出結果.
x,在Rt△AEM中,由三角函數的定義即可得出結果.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
【題目】如圖,點A的坐標為(0,1),點B是x軸正半軸上的一動點,以AB為邊作等腰直角△ABC,使∠BAC=90°,設點B的橫坐標為x,點C的縱坐標為y,能表示y與x的函數關系的圖象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校計劃購買一批課外讀物,為了了解學生對課外讀物的需求情況,學校進行了一次“我最喜愛的課外讀物”的調查,設置了“文學”、“科普”、“藝術”和“其他”四個類別,規定每人必須并且只能選擇其中一類,現從全體學生的調查表中隨機抽取了部分學生的調查表進行統計,并把統計結果繪制了如圖所示的兩幅不完整的統計圖,則在扇形統計圖中,藝術類讀物所在扇形的圓心角是度.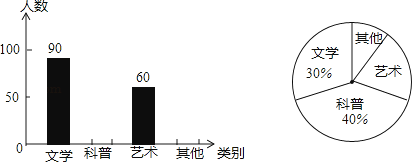
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次中學生田徑運動會上,根據參加男子跳高初賽的運動員的成績(單位:m),繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題: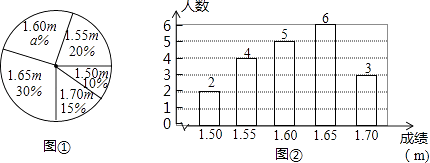
(1)圖1中a的值為;
(2)求統計的這組初賽成績數據的平均數、眾數和中位數;
(3)根據這組初賽成績,由高到低確定9人進入復賽,請直接寫出初賽成績為1.65m的運動員能否進入復賽.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在Rt△ABC中,∠ABC=90°,點D沿BC自B向C運動(點D與點B、C不重合),作BE⊥AD于E,CF⊥AD于F,則BE+CF的值( ) 
A.不變
B.增大
C.減小
D.先變大再變小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖示我國漢代數學家趙爽在注解《周脾算經》時給出的“趙爽弦圖”,圖中的四個直角三角形是全等的,如果大正方形ABCD的面積是小正方形EFGH面積的13倍,那么tan∠ADE的值為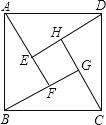
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為4的正方形ABCD中,P是BC邊上一動點(不含B、C兩點),將△ABP沿直線AP翻折,點B落在點E處;在CD上有一點M,使得將△CMP沿直線MP翻折后,點C落在直線PE上的點F處,直線PE交CD于點N,連接MA,NA.則以下結論中正確的有(寫出所有正確結論的序號)
①△CMP∽△BPA;
②四邊形AMCB的面積最大值為10;
③當P為BC中點時,AE為線段NP的中垂線;
④線段AM的最小值為2 ![]() ;
;
⑤當△ABP≌△ADN時,BP=4 ![]() ﹣4.
﹣4.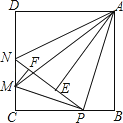
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com