
【題目】如圖,在平面直角坐標系中,![]() 為坐標原點,
為坐標原點,![]() 的邊
的邊![]() 垂直
垂直![]() 軸于點
軸于點![]() ,反比例函數
,反比例函數![]()
![]() 的圖象經過
的圖象經過![]() 的中點
的中點![]() ,與邊
,與邊![]() 相交于點
相交于點![]() ,
,![]() .
.
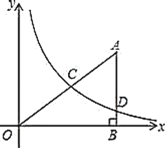
(1)求反比例函數![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)經過![]() 、
、![]() 兩點的直線的解析式是__________.
兩點的直線的解析式是__________.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)設點D的坐標為(4,m)(m>0),則點A的坐標為(4,3+m),由點A的坐標表示出點C的坐標,根據C、D點在反比例函數圖象上結合反比例函數圖象上點的坐標特征即可得出關于k、m的二元一次方程,解方程即可得出結論;
(2)由m的值,可找出點A的坐標,由此即可得出線段OB、AB的長度,通過解直角三角形即可得出結論;
(3)由m的值,可找出點C、D的坐標,設出過點C、D的一次函數的解析式為y=ax+b,由點C、D的坐標利用待定系數法即可得出結論.
解:(1)∵點![]() 的坐標為
的坐標為![]() ,則點
,則點![]() 的坐標為
的坐標為![]() ,
,
∵點![]() 為線段
為線段![]() 的中點,∴點
的中點,∴點![]() 的坐標為
的坐標為![]() .
.
∵點![]() 、點
、點![]() 均在反比例函數
均在反比例函數![]() 的函數圖象上,
的函數圖象上,
∴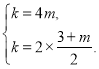 解得:
解得:![]()
∴反比例函數的解析式為![]() ;
;
(2)∵m=1,
∴點A的坐標為(4,4),
∴OB=4,AB=4.
在Rt△ABO中,OB=4,AB=4,∠ABO=90°,
∴OA=![]() ,cos∠OAB=
,cos∠OAB=![]() .
.
(3))∵m=1,
∴點C的坐標為(2,2),點D的坐標為(4,1).
設經過點C、D的一次函數的解析式為y=ax+b,
則有![]() ,解得:
,解得: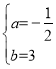 .
.
∴經過C、D兩點的一次函數解析式為y=-![]() x+3.
x+3.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源: 題型:
【題目】為了慶祝中華人民共和國成立70周年,某市決定開展“我和祖國共成長”主題演講比賽,某中學將參加本校選拔賽的40名選手的成績(滿分為100分,得分為正整數且無滿分,最低為75分)分成五組,并繪制了下列不完整的統計圖表.
分數段 | 頻數 | 頻率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
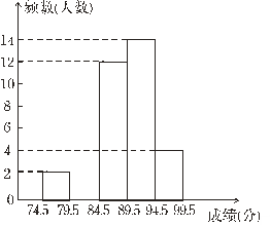
(1)表中m= ,n= ;
(2)請在圖中補全頻數直方圖;
(3)甲同學的比賽成績是40位參賽選手成績的中位數,據此推測他的成績落在 分數段內;
(4)選拔賽中,成績在94.5分以上的選手,男生和女生各2人,學校從中隨機確定2名選手參加全市決賽,恰好是一名男生和一名女生的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,△BPC是等邊三角形,BP、CP的延長線分別交AD于點E、F,連結BD、DP,BD與CF相交于點H.給出下列結論:
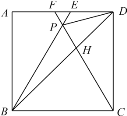
①△ABE≌△DCF;②∠PDF=15°;③![]() ;④
;④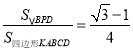 ,其中正確的結論有( )
,其中正確的結論有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
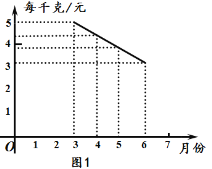
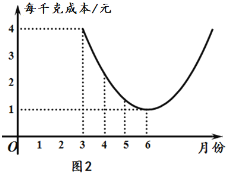
【題目】某種蔬菜的銷售單價y1與銷售月份x之間的關系如圖1所示,成本y2與銷售月份x之間的關系如圖2所示.
(1)已知6月份這種蔬菜的成本最低,此時出售每干克的收益是多少元?(收益=售價-成本)
(2)分別求出y1、y2與x之間的函數關系式;
(3)哪個月出售這種蔬菜,每千克的收益最大?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,點
中,點![]() 為AC邊中點,動點
為AC邊中點,動點![]() 從點
從點![]() 出發,沿著
出發,沿著![]() 的路徑以每秒1個單位長度的速度運動到
的路徑以每秒1個單位長度的速度運動到![]() 點,在此過程中線段
點,在此過程中線段![]() 的長度
的長度![]() 隨著運動時間
隨著運動時間![]() 變化的函數關系如圖2所示,則邊
變化的函數關系如圖2所示,則邊![]() 的長為__________.
的長為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=10,點D是BC邊上的一動點(不與B、C重合),∠ADE=∠B=∠α,DE交AB于點E,且tan∠α=0.75,有以下的結論:
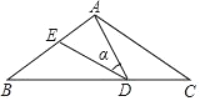
①△DBE∽△ACD;②△ADE∽△ACD;③△BDE為直角三角形時,BD為8或3.5;
④0<BE≤5.其中正確的結論是_______(填入正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某建筑物![]() 上掛著“巴山渝水,魅力重慶”的宣傳條幅
上掛著“巴山渝水,魅力重慶”的宣傳條幅![]() ,王同學利用測傾器在斜坡的底部
,王同學利用測傾器在斜坡的底部![]() 處測得條幅底部
處測得條幅底部![]() 的仰角為60°,沿斜坡AB走到B處測得條幅頂部C的仰角為50°.已知斜坡
的仰角為60°,沿斜坡AB走到B處測得條幅頂部C的仰角為50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(點
米(點![]() 在同平面內,
在同平面內,![]() ,測傾器的高度忽略不計),則條幅
,測傾器的高度忽略不計),則條幅![]() 的長度約為(參考數據:
的長度約為(參考數據:![]()
![]() )
)
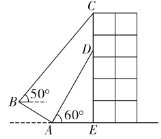
A.12.5米B.12.8米C.13.1米D.13.4米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在ABCD中,E為AD的中點,CE的延長線交BA的延長線于點F,則下列選項中的結論錯誤的是( )
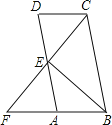
A. FA:FB=1:2 B. AE:BC=1:2
C. BE:CF=1:2 D. S△ABE:S△FBC=1:4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com