
【題目】根據要求進行計算:
(1)計算: ![]() +(﹣2017)0﹣4sin45°
+(﹣2017)0﹣4sin45°
(2)化簡:m(1﹣m)+(m﹣2)2 .
【答案】
(1)解:原式=2 ![]() +1﹣4×
+1﹣4× ![]() =2
=2 ![]() +1﹣2
+1﹣2 ![]() =1;
=1;
(2)解:原式=m﹣m2+m2﹣4m+4
=﹣3m+4.
【解析】(1)原式第一項化為最簡二次根式,第二項利用零指數冪法則計算,最后一項利用特殊角的三角函數值計算即可得到結果.(2)根據整式的運算法則:先算乘除,再算加減,即可求得答案.
【考點精析】掌握零指數冪法則和特殊角的三角函數值是解答本題的根本,需要知道零次冪和負整數指數冪的意義: a0=1(a≠0);a-p=1/ap(a≠0,p為正整數);分母口訣:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口訣:“123,321,三九二十七”.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
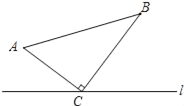
【題目】如圖,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm.動點P從A點出發沿A→C的路徑向終點C運動;動點Q從B點出發沿B→C→A路徑向終點A運動.點P和點Q分別以每秒1cm和3cm的運動速度同時開始運動,其中一點到達終點時另一點也停止運動,在某時刻,分別過點P和Q作PE⊥MN于E,QF⊥MN于F.則點P運動時間為_____秒時,△PEC與△QFC全等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算或化簡
(1)![]() ; (2)(﹣2a2)(3ab2﹣5ab3)
; (2)(﹣2a2)(3ab2﹣5ab3)
(3)(x+3)(x﹣7)﹣x(x﹣1). (4)(a﹣2b+1)(a+2b+1)
(5)(3a﹣b)2﹣(2a+b)2﹣5a(a﹣b) (6)(x+2y)2(x﹣2y)2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司推銷一種產品,公司付給推銷員的月報酬有兩種方案如圖所示:其中方案一所示圖形是頂點B在原點的拋物線的一部分,方案二所示圖形是射線.設推銷員推銷產品的數量為x(件),付給推銷員的月報酬為y(元).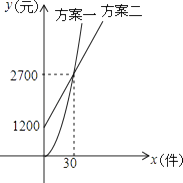
(1)分別求兩種方案中y關于x的函數關系式;
(2)當銷售達到多少件時,兩種方案月報酬差額將達到3800元?
(3)若公司決定改進“方案二”:保持基本工資不變,每件報酬增加m元,使得當銷售員銷售產量達到40件時,兩種方案的報酬差額不超過1000元.求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是矩形,延長AB至點F,連結CF,使得CF=AF,過點A作AE⊥FC于點E. 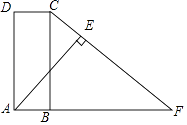
(1)求證:AD=AE.
(2)連結CA,若∠DCA=70°,求∠CAE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知A(0,a),B(b,0),C(b,4)三點,其中a,b滿足關系式a=![]() +2.若在第二象限內有一點P(m,1),使四邊形ABOP的面積與三角形ABC的面積相等,則點P的坐標為( )
+2.若在第二象限內有一點P(m,1),使四邊形ABOP的面積與三角形ABC的面積相等,則點P的坐標為( )
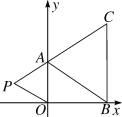
A. (-3,1) B. (-2,1) C. (-4,1) D. (-2.5,1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O是坐標原點,菱形OABC的頂點A的坐標為(﹣3,4),頂點C在x軸的負半軸上,函數y= ![]() (x<0)的圖象經過頂點B,則k的值為( )
(x<0)的圖象經過頂點B,則k的值為( ) 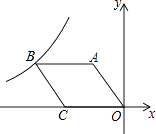
A.﹣12
B.﹣27
C.﹣32
D.﹣36
查看答案和解析>>
科目:初中數學 來源: 題型:
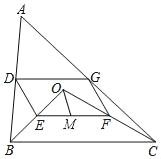
【題目】如圖,點O是△ABC內一點,連接OB,OC,并將AB,OB,OC,AC的中點D,E,F,G依次連接得到四邊形DEFG.
(1)求證:四邊形DEFG是平行四邊形;
(2)若OB⊥OC,∠EOM和∠OCB互余,OM=3,求DG的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com