
【題目】計算:
(1)解方程組: 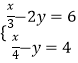
(2)求不等式﹣2< ![]() ≤2的整數解.
≤2的整數解.
【答案】
(1)解:  ,①﹣②×2得,﹣x=﹣12,解得x=12,
,①﹣②×2得,﹣x=﹣12,解得x=12,
把x=12代入①得,4﹣2y=6,解得y=﹣1,
故方程組的解為: ![]()
(2)解:原不等式化為不等式組  ,
,
解①得,x>﹣ ![]() ,解②得,x≤
,解②得,x≤ ![]() ,
,
所以不等式組的解集為,﹣ ![]() <x≤
<x≤ ![]() .
.
所以,原不等式的整數解是﹣4,﹣3,﹣2,﹣1,0,1
【解析】(1)先用加減消元法求出x的值,再用代入消元法求出y的值即可;(2)把不等式化為不等式組的形式,分別求出各不等式的解集,再求出其公共解集即可.
【考點精析】本題主要考查了解二元一次方程組和一元一次不等式組的整數解的相關知識點,需要掌握二元一次方程組:①代入消元法;②加減消元法;使不等式組中的每個不等式都成立的未知數的值叫不等式組的解,一個不等式組的所有的解組成的集合,叫這個不等式組的解集(簡稱不等式組的解)才能正確解答此題.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=2,且拋物線經過A(-1,0),C(0,-5)兩點,與x軸交于點B.
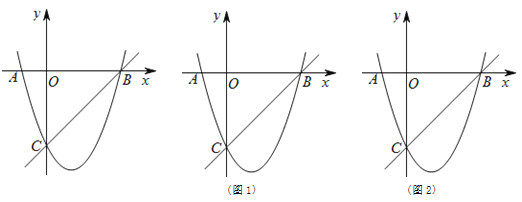
(1)若直線y=mx+n經過B、C兩點,求直線BC和拋物線的解析式;
(2)設點P為拋物線上的一個動點,連接PB、PC,若△BPC是以BC為直角邊的直角三角形,求此時點P的坐標;
(3)在拋物線上BC段有另一個動點Q,以點Q為圓心作⊙Q,使得⊙Q與直線BC相切,在運動的過程中是否存在一個最大⊙Q. 若存在,請直接寫出最大⊙Q的半徑;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場對今年端午節這天銷售A、B、C三種品牌粽子的情況進行了統計,繪制如圖1和2所示的統計圖.根據圖中信息解答下列問題: 
(1)這天共銷售了多少個粽子?
(2)銷售品牌粽子多個個?并補全圖1中的條形圖;
(3)求出A品牌粽子在圖2中所對應的圓心角的度數;
(4)根據上述統計信息,明年端午節期間該商場對A、B、C三種品牌的粽子如何進貨?請你提一條合理化的建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
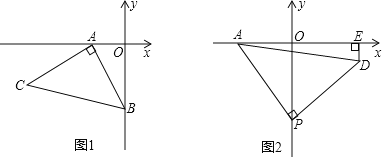
【題目】如圖1,OA=1,OB=3,以A為直角頂點,AB為腰在第三象限作等腰Rt△ABC.
(1)求點C的坐標;
(2)如圖2,P為y軸負半軸上的一個動點,當點P向下運動時,以P點為直角頂點,PA為腰作等腰Rt△APD,過D作DE⊥x軸于E點,求PO-DE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個盒子里裝有標號為1,2,3,4,5,6,7,8,9,10的十個小球,這些小球除標號數字之外都相同,甲,乙二人用這些小球玩游戲,規則是:甲、乙先后從盒子里摸球(不放回),誰摸到的標號數字大,誰就獲勝.
(1)第一輪游戲:若甲先摸到了1號球,求甲獲勝的概率;
(2)第二輪游戲:若甲先摸到了10號球,求甲獲勝的概率;
(3)第三輪游戲:若甲先摸到了3號球,那么甲、乙獲勝的概率分別是多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程ax2+bx+c=5的一個根是2,且二次函數y=ax2+bx+c的對稱軸是直線x=2,則拋物線y=ax2+bx+c的頂點坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學舉行了一次演講比賽,分段統計參賽同學的成績,結果如下表(滿分100分)
分數段/分 | 61~70 | 71~80 | 81~90 | 91~100 |
人數/人 | 2 | 8 | 6 | 4 |
若已知成績在91-100分的同學為優勝者.那么優勝率為%。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知y﹣3與3x+1成正比例,且x=2時,y=6.5.
(1)求y與x之間的函數關系式,并指出它是什么函數;
(2)若點(a,2)在這個函數的圖象上,求a.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com