
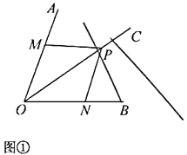
【題目】問題呈現:下圖是小明復習全等三角形時遇到的一個問題并引發的思考,請幫助小明完成以下學習任務.

請根據小明的思路,結合圖①,寫出完整的證明過程.結論應用:
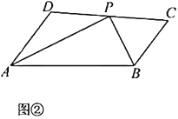
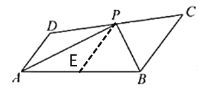
(1)如圖②,在四邊形![]() 中,
中,![]() ,
,![]() 的平分線和
的平分線和![]() 的平分線交于
的平分線交于![]() 邊上點
邊上點![]() .求證:
.求證:![]() ;
;
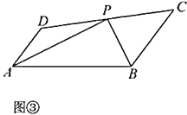
(2)在(1)的條件下,如圖③,若![]() ,
,![]() .當
.當![]() 有一個內角是
有一個內角是![]() 時,
時,![]() 的面積是 .
的面積是 .
【答案】問題呈現:見解析;結論應用:(1)見解析;(2)![]() 或8
或8
【解析】
問題呈現:由“SAS”可證△MOP≌△NOP,可得PM=PN;
結論應用:(1)在AB上截取AE=AD,連接PE,由“SAS”可證△ADP≌△AEP,△BPC≌△BPE,可得PD=PE=PC;(2)延長AP,BC交于點H,由“ASA”可證△ADP≌△HCP,可得CP=DP,AD=CH,S△ADP=S△CPH,分三種情況討論,由角平分線的性質和銳角三角函數可求解.
問題呈現:
證明:∵![]() 平分
平分![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
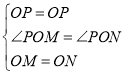 .
.
∴![]() .
.
結論應用:
在![]() 上截取
上截取![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∵![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)由(1)可證∠D=∠AEP,∠PCB=∠PEB,
∵∠AEP+∠PEB=180°,
∴∠PCB+∠D=180°,
∴AD∥BC,
∵AB=10,tan∠PAB=![]() =
=![]() ,
,
∴PA=2PB,
∵PA2+PB2=AB2,
∴PB=2![]() ,PA=4
,PA=4![]() ,
,
如圖③,延長AP,BC交于點H,

∵AD∥BC,
∴∠DAP=∠H,
∴∠H=∠BAP,
∴AB=BH=10,
又∵PB平分∠ABC,
∴BP⊥AP,AP=PH=4![]() ,
,
∵∠DAP=∠H,AP=PH,∠DPA=∠CPH,
∴△ADP≌△HCP(ASA),
∴CP=DP,AD=CH,S△ADP=S△CPH,
若∠PBC=45°時,則∠PBC=∠H=45°,
∴PB=PH(不合題意舍去),
若∠BPC=45°時,則∠HPC=∠BPC=45°,
如圖④,過點C作CN⊥BP于N,CM⊥PH于M,
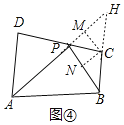
∴CM=CN,
∵S△PBH=![]() ×BP×PH=
×BP×PH=![]() ×BP×CN+
×BP×CN+![]() ×PH×CM,
×PH×CM,
∴CM=CN=![]() ,
,
∴S△PCH=![]() ×4
×4![]() ×
×![]() =
=![]() =S△ADP;
=S△ADP;
若∠PCB=45°時,
如圖⑤,過點P作PF⊥BC于F,
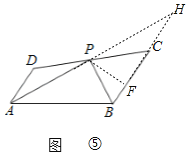
∵∠PAB=∠H,
∴tanH=tan∠PAB=![]() ,
,
∴![]() ,
,
∴FH=2PF,
∵PF2+FH2=PH2=80,
∴PF=4,FH=8,
∵PF⊥BC,∠BCP=45°,
∴∠PCB=∠FPC=45°,
∴CF=PF=4,
∴CH=4,
∴S△ADP=S△CPH=![]() ×4×4=8,
×4×4=8,
故答案為:8或![]() .
.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案科目:初中數學 來源: 題型:
【題目】截至北京時間2020年3月22日14時30分,全球新冠肺炎確診病例達305740例,超過30萬,死亡病例累計12762人,將“305740”這個數字用科學記數法表示保留兩位有效數字為( )
A.3.05740×105B.3.05×105C.3.0×105D.3.1×105
查看答案和解析>>
科目:初中數學 來源: 題型:
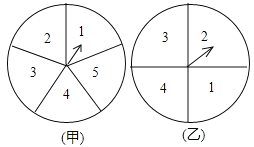
【題目】小明和小亮用如圖所示的甲、乙兩個轉盤(甲轉盤被分成五個面積相等的扇形,乙轉盤被分成四個面積相等的扇形)做游戲,轉動兩個轉盤各一次(如果指針恰好在分割線上,那么重轉一次,直到指針指向某一扇形區域為止).
(1)請你求出甲轉盤指針指向偶數區域的概率;
(2)若兩次數字之和為![]() ,
,![]() 或
或![]() 時,則小明勝,否則小亮勝,這個游戲對雙方公平嗎?請你用樹狀圖或列表法說說你的理由.
時,則小明勝,否則小亮勝,這個游戲對雙方公平嗎?請你用樹狀圖或列表法說說你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了參加學校舉行的傳統文化知識競賽,某班進行了四次模擬訓練,將成績優秀的人數和優秀率繪制成如下兩個不完整的統計圖:
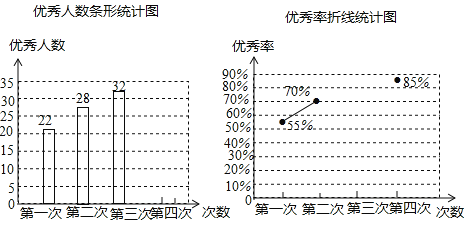
(1)求該班總人數;
(2)根據計算,請你補全兩個統計圖;
(3)已知該班甲同學四次訓練成績為85,95,85,95,乙同學四次成績分別為85,90,95,90,現需從甲、乙兩同學中選派一名同學參加校級比賽,你認為應該選派哪位同學并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組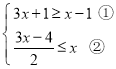 ,請結合題意填空,完成本題的解答.
,請結合題意填空,完成本題的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在數軸上表示出來:
![]()
(4)原不等式組的解集為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,一塊四邊形紙板剪去![]() ,得到四邊形
,得到四邊形![]() ,測得
,測得![]() ,
,![]() ,
,![]() .能否在四邊形紙板
.能否在四邊形紙板![]() 上只剪一刀,使剪下的三角形與
上只剪一刀,使剪下的三角形與![]() 全等?請說明理由.
全等?請說明理由.
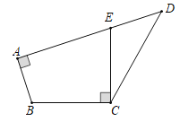
(2)我市某學校八年級同學乘坐大巴車去長江青少年素質教育實踐基地參加綜合實踐活動.1號車出發4分鐘后,2號車才出發,結果兩車同時到達.已知素質教育基地距離該校18千米,2號車的平均速度是1車的平均速度的![]() 倍.請你就“1號車”提出一個用分式方程解決的問題,并寫出解題過程.
倍.請你就“1號車”提出一個用分式方程解決的問題,并寫出解題過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com