
【題目】已知△ABC與△CEF均為等腰直角三角形,∠ABC=∠CFE=90°,連接AE,點G是AE中點,連接BG和GF.
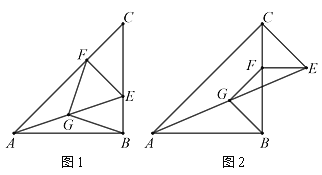
(1)如圖1,當△CEF中E、F落在BC、AC邊上時,探究FG與BG的關系;
(2)如圖2,當△CEF中F落在BC邊上時,探究FG與BG的關系.
【答案】(1) FG=BG,FG⊥BG;證明見詳解;(2)FG=BG,FG⊥BG;證明見詳解;
【解析】
(1)由∠AFE=∠ABE=90°,點G是AE中點,則![]() ,
,![]() ,則得到FG=BG,∠FGE=2∠FAG,∠BGE=2∠BAG,由∠FAG+∠BAG=45°,即可得到∠BGF=90°;
,則得到FG=BG,∠FGE=2∠FAG,∠BGE=2∠BAG,由∠FAG+∠BAG=45°,即可得到∠BGF=90°;
(2)過點E作ED⊥AB,交AB延長線于點D,連接DG,CG,根據題意,找出相應的條件證明△GFE≌△GBD(SAS),得到FG=BG,與(1)證法一樣,證明∠CGD=90°,通過等量代換即可得到∠FGB=90°.
解:(1)FG=BG,FG⊥BG;如圖1,
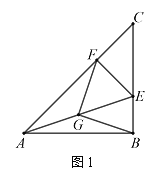
∵∠ABC=∠CFE=90°,
∴△ABE和△AFE是直角三角形,
∵點G是AE的中點,
∴![]() ,
,![]() ,
,
∴![]() .,∠GAF=∠GFA,∠GAB=∠GBA,
.,∠GAF=∠GFA,∠GAB=∠GBA,
∴∠FGE=2∠FAG,∠BGE=2∠BAG,
∵∠BAC=∠FAG+∠BAG=45°
∴∠BGF=∠FGE+∠BGE=2(∠FAG+∠BAG)=90°,
即FG⊥BG;
(2)![]() ,
,![]() ;
;
過點E作ED⊥AB,交AB延長線于點D,連接DG,CG,
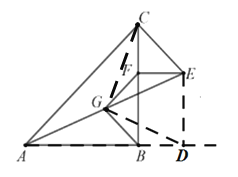
∵△ABC與△CEF均為等腰直角三角形,ED⊥AB,
∴∠FBD=∠BFE=∠EDB=90°,
∴四邊形BFED是矩形,
∴BD=EF,
在直角三角形ADE和直角三角形ACE中,G是AE中點,
∴DG=GE=AG=CG=![]() ,
,
∴∠GED=∠GDE,
∴∠FEG=∠BDG,
∴△GFE≌△GBD(SAS),
∴GF=GB,CF=BD,
∵DG=AG=CG,
∴△CGF≌△DGB,∠CAG=∠ACG,∠DAG=∠ADG,
∴∠CGF=∠DGB,
∵∠CAG+∠DAG=45°,
∠CGE+∠DGE=2(∠CAG+∠DAG)=90°,
即∠CGD=90°,
∴∠CGD-∠CGF+∠DGB=∠FGB=90°,
即FG⊥BG.


科目:初中數學 來源: 題型:
【題目】為提高飲水質量,越來越多的居民開始選購家用凈水器.一商家抓住商機,從廠家購進了A、B兩種型號家用凈水器共160臺,A型號家用凈水器進價是150元/臺,B型號家用凈水器進價是350元/臺,購進兩種型號的家用凈水器共用去36000元.
(1)求A、B兩種型號家用凈水器各購進了多少臺;
(2)為使每臺B型號家用凈水器的毛利潤是A型號的2倍,且保證售完這160臺家用凈水器的毛利潤不低于11000元,求每臺A型號家用凈水器的售價至少是多少元?(注:毛利潤=售價﹣進價)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,其中A點坐標為(-1,0),B點坐標為(5,0)點C(0,5),M為它的頂點.
(1)求拋物線的解析式;
(2)求△MAB的面積。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小區將原來400平方米的正方形場地改建成300平方米的長方形場地,且長和寬之比為3∶2.如果把原來正方形場地的鐵柵欄圍墻利用起來圍成新場地的長方形圍墻,那么這些鐵柵欄是否夠用?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足為A,B,連接AB,下列結論中不一定成立的是( )

A.PA=PBB.PO平分∠APBC.OA=OBD.AB平分OP
查看答案和解析>>
科目:初中數學 來源: 題型:
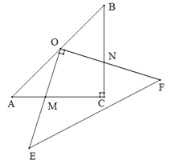
【題目】如圖,在Rt△ACB中,AC=BC=8,O為AB的中點,以O為直角頂點作等腰直角三角形OEF,與邊AC,BC相交于點M,N.有下列結論:①AM=CN;②CM+CN=8;③![]() ;④當M是AC的中點時,OM=ON.其中正確結論的序號是______.
;④當M是AC的中點時,OM=ON.其中正確結論的序號是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解八年級學生對![]() (科學)、
(科學)、![]() (技術)、
(技術)、![]() (工程)、
(工程)、![]() (藝術)、
(藝術)、![]() (數學)中哪一個領域最感興趣的情況,該校對八年級學生進行了抽樣調查,根據調查結果繪制成如下的條形圖和扇形圖,請根據圖中提供的信息,解答下列問題:
(數學)中哪一個領域最感興趣的情況,該校對八年級學生進行了抽樣調查,根據調查結果繪制成如下的條形圖和扇形圖,請根據圖中提供的信息,解答下列問題:

(1)這次抽樣調查共調查了多少名學生?
(2)補全條形統計圖;
(3)求扇形統計圖中![]() (數學)所對應的圓心角度數;
(數學)所對應的圓心角度數;
(4)若該校八年級學生共有400人,請根據樣本數據估計該校八年級學生中對![]() (科學)最感興趣的學生大約有多少人?
(科學)最感興趣的學生大約有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com