
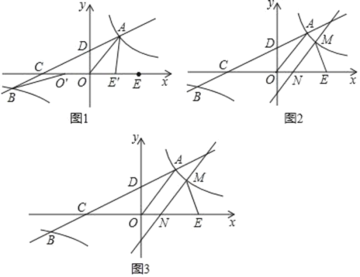
【題目】如圖1,在平面直角坐標系xOy中,雙曲線![]() 與直線y=ax+b(a≠0)交于A、B兩點,直線AB分別交x軸、y軸于C、D兩點,E為x軸上一點.已知OA=OC=OE,A點坐標為(3,4).
與直線y=ax+b(a≠0)交于A、B兩點,直線AB分別交x軸、y軸于C、D兩點,E為x軸上一點.已知OA=OC=OE,A點坐標為(3,4).
(1)將線段OE沿x軸平移得線段O′E′(如圖1),在移動過程中,是否存在某個位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此時點O′的坐標;若不存在,請說明理由;
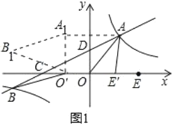
(2)將直線OA沿射線OE平移,平移過程中交![]() 的圖象于點M(M不與A重合),交x軸于點N(如圖3).在平移過程中,是否存在某個位置使△MNE為以MN為腰的等腰三角形?若存在,求出M的坐標;若不存在,請說明理由.
的圖象于點M(M不與A重合),交x軸于點N(如圖3).在平移過程中,是否存在某個位置使△MNE為以MN為腰的等腰三角形?若存在,求出M的坐標;若不存在,請說明理由.
【答案】(1)存在,|BO′﹣AE′|的最大值為![]() ,此時點O′的坐標(﹣
,此時點O′的坐標(﹣![]() ,0);(2)存在,M(
,0);(2)存在,M(![]() )或(8,
)或(8,![]() ).
).
【解析】
(1)把A向左平移5個單位得A1(-2,4),作B關于x軸的對稱點B1,則有|BO′-AE′|=|BO′-A1O′|=B1O′-A1O′|≤A1B1,想辦法求出A1B1,直線A1B1的解析式即可解決問題;
(2)設M(m,![]() ),則N(m
),則N(m![]() ,0),NE2=(5-m+
,0),NE2=(5-m+![]() )2,ME2=(5-m)2+(
)2,ME2=(5-m)2+(![]() )2,MN2=(
)2,MN2=(![]() )2+(
)2+(![]() )2,分MN=EM,MN=NE兩種情形,分別構建方程即可解決問題.
)2,分MN=EM,MN=NE兩種情形,分別構建方程即可解決問題.
(1)如圖1中,
∵A(3,4),
∴OA=![]() =5,
=5,
∵OA=OC=OE,
∴OA=OC=OE=5,
∴C(﹣5,0),E(5,0),
把A、C兩點坐標代入y=ax+b得到![]() ,
,
解得![]() ,
,
∴直線的解析式為:![]() ,
,
把A(3,4)代入y=![]() 中,得到k=12,
中,得到k=12,
∴反比例函數的解析式為y=![]() ,
,
把A向左平移5個單位得A1(﹣2,4),作B關于x軸的對稱點B1,
則有|BO′﹣AE′|=|BO′﹣A1O′|=|B1O′﹣A1O′|≤A1B1,
直線AC:![]() ,
,
雙曲線:![]() ,
,
∴B(﹣8,﹣![]() ),B1(﹣8,
),B1(﹣8,![]() ),
),
∴A1B1=![]() ,
,
直線A1B1:![]() ,
,
令y=0,可得x=﹣![]() ,
,
∴O′(﹣![]() ,0).
,0).
∴|BO′﹣AE′|的最大值為![]() ,此時點O′的坐標(﹣
,此時點O′的坐標(﹣![]() ,0).
,0).
(2)設M(m,![]() ),則N(m﹣
),則N(m﹣![]() ,0),
,0),
∴NE2=(5﹣m+![]() )2,ME2=(5﹣m)2+(
)2,ME2=(5﹣m)2+(![]() )2,MN2=(
)2,MN2=(![]() )2+(
)2+(![]() )2
)2
若MN=ME,則有,(5﹣m)2+(![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得:m=![]() 或
或![]() (舍棄),
(舍棄),
∴M(![]() ,
,![]() ),
),
若MN=NE,則有(5﹣m+![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,解得m=8或3(舍棄),
)2,解得m=8或3(舍棄),
∴M(8,![]() ),
),
綜上所述,滿足條件的點M的坐標為(![]() ,
,![]() )或(8,
)或(8,![]() ).
).


 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
【題目】兩個全等的等腰直角三角形按如圖方式放置在平面直角坐標系中,OA在x軸上,已知∠COD=∠OAB=90°,OC=![]() ,反比例函數y=
,反比例函數y=![]() 的圖象經過點B.
的圖象經過點B.
(1)求k的值.
(2)把△OCD沿射線OB移動,當點D落在y=![]() 圖象上時,求點D經過的路徑長.
圖象上時,求點D經過的路徑長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() 中,
中,![]() ,P是斜邊AC上一個動點,以即為直徑作
,P是斜邊AC上一個動點,以即為直徑作![]() 交BC于點D,與AC的另一個交點E,連接DE.
交BC于點D,與AC的另一個交點E,連接DE.
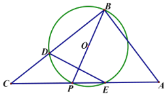
(1)當![]() 時,
時,
①若![]() ,求
,求![]() 的度數;
的度數;
②求證![]() ;
;
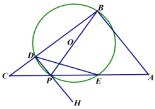
(2)當![]() ,
,![]() 時,
時,
①是含存在點P,使得![]() 是等腰三角形,若存在求出所有符合條件的CP的長;
是等腰三角形,若存在求出所有符合條件的CP的長;
②以D為端點過P作射線DH,作點O關于DE的對稱點Q恰好落在![]() 內,則CP的取值范圍為________.(直接寫出結果)
內,則CP的取值范圍為________.(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),AB=CD,AD=BC,O為AC中點,過O點的直線分別與AD、BC相交于點M、N,那么∠1與∠2有什么關系?請說明理由;
若過O點的直線旋轉至圖(2)、(3)的情況,其余條件不變,那么圖(1)中的∠1與∠2的關系成立嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
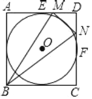
【題目】如圖,⊙O內切于正方形ABCD,邊AD、CD分別與⊙O切于點E、F,點M、N分別在線段DE、DF上,且MN與⊙O相切,若△MBN的面積為8,則⊙O的半徑為( )
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品現在的售價為每件60元,每星期可賣出300件. 市場調查反映:如調整價格,每降價1元,每星期可多賣出20件. 已知商品的進價為每件40元,如何定價才能使利潤最大?這個最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題:
“美化城市,改善人民居住環境”是城市建設的一項重要內容.某市近年來,通過植草、栽樹、修建公園等措施,使城區綠地面積不斷增加,2011年底該市城區綠地總面積約為75公頃,截止到2013年底,該市城區綠地總面積約為108公頃,求從2011年底至2013年底該市城區綠地總面積的年平均增長率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形紙片ABCD中,AB=4,AD=6,點P是邊BC上的動點,現將紙片折疊,使點A與點P重合,折痕與矩形邊的交點分別為E、F,要使折痕始終與邊AB、AD有交點,則BP的取值范圍是_________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在初中階段的函數學習中,我們經歷了“確定函數的解析式利用函數圖象研究其性質﹣運用函數解決問題”的學習過程.在畫函數圖象時,我們可以通過描點或平移或翻折等方法畫出函數圖象、下面我們対函數y=|![]() ﹣1|展開探索,請補充以下探索過程:
﹣1|展開探索,請補充以下探索過程:
(1)列表
x | … | ﹣1 | ﹣ | ﹣ | ﹣ | 0 |
|
|
| … |
|
|
| 2 |
|
|
| 3 | … | |
y | … |
|
|
|
| 2 |
| 3 | a | … | 3 | 1 |
| 0 |
|
| b |
| … | |
直接寫出函數自變量x的取值范圍,及a= ,b= ;
(2)在給出的平面直角坐標系中,請用你喜歡的方法畫出這個函數的圖象,并寫出這個函數的一條性質: .
(3)若方程|![]() ﹣1|=m有且只有一個解,直接寫出m的值: .
﹣1|=m有且只有一個解,直接寫出m的值: .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com