
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上運動(
上運動(![]() 不與
不與![]() ,
,![]() 重合),連接
重合),連接![]() ,
,![]() ,
,![]() 交線段
交線段![]() 于
于![]() .
.
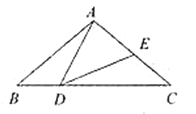
(1)當![]() 時,
時,![]() ______
______![]() ,
,![]() ______
______![]() ,點
,點![]() 從
從![]() 向
向![]() 運動時,
運動時,![]() 逐漸變______(填“大”或“小”);
逐漸變______(填“大”或“小”);
(2)當![]() 等于多少時,
等于多少時,![]() 與
與![]() 全等?請說明理由.
全等?請說明理由.
【答案】(1)![]() ,
,![]() ,小;(2)
,小;(2)![]() .
.
【解析】
(1)根據三角形內角和定理,將已知數值代入即可求出∠BAD;根據平角求出∠EDC的度數,根據AB=AC可得∠C的度數,根據三角形內角和定理即可求出∠DEC;根據點D的運動方向可判定∠BDA的變化情況.
(2)當DC=2時,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
解:(1)∠BAD=180°-∠ABD-∠BDA=180°-40°-115°=25°;
∵AB=AC,
∴∠C=∠B=40°
∵∠EDC=180°-∠ADE-∠BDA=180°-40°-115°=25°,
∴∠DEC=180°-∠EDC -∠C=180°-25°-40°=115°;
從圖中可以得知,點D從B向C運動時,∠BDA逐漸變小;
故答案為:![]() ,
,![]() ,小;
,小;

(2)當![]() 時,
時,![]() .理由如下:
.理由如下:
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
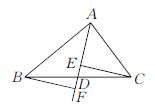
【題目】如圖,在△ABC中,點D是BC的中點,作射線AD,在線段AD及其延長線上分別取點E,F,連結CE,BF.添加一個條件,使得△BDF≌△CDE,你添加的條件是_____________________(不添加輔助線).
查看答案和解析>>
科目:初中數學 來源: 題型:
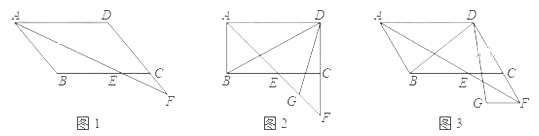
【題目】在平行四邊形ABCD中,E是BC上任意一點,延長AE交DC的延長線與點F.
(1)在圖中當CE=CF時,求證:AF是∠BAD的平分線.
(2)在(1)的條件下,若∠ABC=90°,G是EF的中點(如圖),請求出∠BDG的度數.
(3)如圖,在(1)的條件下,若∠BAD=60°,且FG∥CE,FG=CE,連接DB、DG,求出∠BDG的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
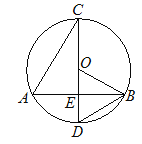
【題目】如圖,CD為⊙O的直徑,弦AB交CD于點E,連接BD、OB.
(1)求證:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半徑.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
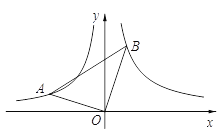
【題目】如圖,∠ AOB=90°,且點A,B分別在反比例函數![]() (x<0),
(x<0),![]() (x>0)的圖象上,且k1,k2分別是方程x2-x-6=0的兩根.
(x>0)的圖象上,且k1,k2分別是方程x2-x-6=0的兩根.
(1)求k1,k2的值;
(2)連接AB,求tan∠ OBA的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,過等邊三角形ABC邊AB上一點D作DE∥BC交邊AC于點E,分別取BC,DE的中點M,N,連接MN.
(1)發現:在圖1中,![]() ,說明理由;
,說明理由;
(2)探索:如圖2,將△ADE繞點A旋轉,請求出![]() 的值;
的值;
(3)拓展:如圖3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分別是底邊BC,DF的中點,若BD⊥CE,請直接寫出![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級學生小陽,小杰和小凡到某超市參加了社會實踐活動,在活動中他們參與了某種水果的銷售工作,已知該水果的進價為10元/千克,下面是他們在活動結束后的對話.
小陽:如果以12元/千克的價格銷售,那么每天可售出300千克.
小杰:如果以15元/千克的價格銷售,那么每天可獲取利潤750元.
小凡:我通過調查驗證發現每天的銷售量y(千克)與銷售單價x(元)之間存在一次函數關系.
(1)求y(千克)與x(元)(x>0)的函數關系式;
(2)當銷售單價為何值時,該超市銷售這種水果每天獲得的利潤達600元?
查看答案和解析>>
科目:初中數學 來源: 題型:
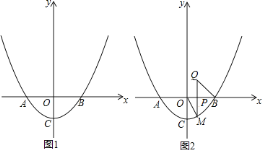
【題目】已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .
.
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 點
點![]() 是第二象限內一點,過點
是第二象限內一點,過點![]() 作
作![]() 軸交拋物線于點
軸交拋物線于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() 、
、![]() ,若
,若![]() .求
.求![]() 的值并直接寫出
的值并直接寫出![]() 的取值范圍(利用圖
的取值范圍(利用圖![]() 完成你的探究).
完成你的探究).
![]() 如圖
如圖![]() ,點
,點![]() 是線段
是線段![]() 上一動點(不包括點
上一動點(不包括點![]() 、
、![]() ),
),![]() 軸交拋物線于點
軸交拋物線于點![]() ,
,![]() ,
,![]() 交直線
交直線![]() 于點
于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,求
,求![]() 的周長.
的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】課間,小聰拿著老師的等腰直角三角板玩,不小心掉到兩墻之間(如圖),![]() ,
,![]() ,從三角板的刻度可知
,從三角板的刻度可知![]() ,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為________
,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為________![]() .
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com