
【題目】學校“百變魔方”社團準備購買![]() 、
、![]() 兩種魔方,已知購買
兩種魔方,已知購買![]() 個
個![]() 種魔方和
種魔方和![]() 個
個![]() 種魔方共需
種魔方共需![]() 元,又知購買
元,又知購買![]() 個
個![]() 種魔方所需款數和購買
種魔方所需款數和購買![]() 個
個![]() 種魔方所需款數相同.
種魔方所需款數相同.
(1)求這兩種魔方的單價;
(2)結合社員們的需求,社團決定購買![]() 、
、![]() 兩種魔方共
兩種魔方共![]() 個.某商店有兩種優惠活動,如圖所示。請根據以上信息,如何購買可以使兩種優惠方案一致.
個.某商店有兩種優惠活動,如圖所示。請根據以上信息,如何購買可以使兩種優惠方案一致.
⑶當購買![]() 種魔方
種魔方![]() 個時該如何花費才能使得所花錢數最少.
個時該如何花費才能使得所花錢數最少.
【答案】(1) A種魔方的單價為20元/個,B種魔方的單價為15元/個;(2) 當買A60個,B40個或A45個,B55個時優惠方案一致;(3) 按活動二買A40個,再按活動一買B20個花錢最少.
【解析】
(1)設A種魔方的單價為x元/個,則B種魔方的單價為y元/個,根據購買2個A種魔方和6個B種魔方共需130元,購買![]() 個
個![]() 種魔方所需款數和購買
種魔方所需款數和購買![]() 個
個![]() 種魔方所需款數相同,即可得出關于x的一元一次方程組,解之即可得出結論;
種魔方所需款數相同,即可得出關于x的一元一次方程組,解之即可得出結論;
(2)設購進A種魔方a個,總價格為w元,則購進B種魔方(100-a)個,根據兩種活動方案即可得出w活動一、w活動二關于a的函數關系式,再分a≥100-a,a<100-a兩種情況,解出a的值即可;
(3)分兩種情況①當a=40時,w活動一=1000元,W活動二=1100,此時活動一優惠②A40個,B60個,先按活動二買A40個,送B40個,再按活動一買B20個,得出結果比較即可.
解:(1)設A種魔方的單價為x元/個,B種魔方的單價為y元/個,
根據題意得:![]() ,
,
解得:![]() .
.
答:A種魔方的單價為20元/個,B種魔方的單價為15元/個.
(2)設購進A種魔方a個,總價格為w元,則購進B種魔方(100-a)個,
根據題意得:w活動一=20a×0.8+15(100-a)×0.4=10a+600;
當a≥100-a時,B全部送,w活動二=20a,此時a≥50,
當a<100-a時,w活動二=20a+15(100-a-a)=-10a+1500,此時a<50,
w活動二![]() ,
,
令w活動一=w活動二,∴10a+600=20a, ∴a=60,100-a=40;
或10a+600=-10a+1500,∴a=45,100-a=55,
∴當買A60個,B40個或A45個,B55個時優惠方案一致.
(3)①當a=40時,w活動一=1000元,
w活動二=-10×40+1500=1100元,
∵1000<1100,
∴選活動一;
②A40個,B60個,先按活動二買A40個,送B40個,再按活動一買B20個,
40×20+20×15×0.4=800+120=920元<1000元,
答:按活動二買A40個,再按活動一買B20個花錢最少.


科目:初中數學 來源: 題型:
【題目】定義符號min{a,b,c}表示a、b、c三個數中的最小值,如min{1,﹣2,3}=﹣2,min{0,5,5}=0.
(1)根據題意填空:min![]() = ;
= ;
(2)試求函數y=min{2,x+1,﹣3x+11}的解析式;
(3)關于x的方程﹣x+m=min{2,x+1,﹣3x+11}有解,試求常數m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,已知AD∥BC,AB⊥BC,點E,F在邊AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
.
(1)BC= ;
(2)求點D到BC的距離;
(3)求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙三位同學分別正確指出了某一個函數的一個性質.甲:函數圖象經過第一象限;乙:函數圖象經過第三象限;丙:每第一個象限內,y值隨x值的增大而減小.根據他們的描述,這個函數表達式可能是( )
A.y=2x
B.y= ![]()
C.y=﹣ ![]()
D.y=2x2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為坐標原點,A(1,3),B(2,1),直角坐標系中存在點C,使得O,A,B,C四點構成平行四邊形,則C點的坐標為______________________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某同學對多項式(x2-4x-3)(x2-4x+1)+4進行因式分解的過程.
解:設x2-4x=y
原式=(y-3)(y+1)+4 (第一步)
= y2-2y+1 (第二步)
=(y-1)2 (第三步)
=(x2-4x-1)2 (第四步)
回答下列問題:
(1)該同學第二步到第三步運用了因式分解的_______.
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)請你模仿以上方法嘗試對多項式(x2+2x)(x2+2x+2)+1進行因式分解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=5,AB=3.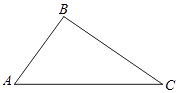
(1)利用尺規在AC上找到一點D,使得DA=DC(保留作圖痕跡,不寫作法).
(2)連接DB,若DA=DC=DB,試判斷△ABC的形狀,說明理由,并求出△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】父親告訴小明:“距離地面越高,溫度越低,”并給小明出示了下面的表格。
距離地面高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
溫度(℃) | 20 | 14 | 8 | 2 |
|
|
根據上表,父親還給小明出了下面幾個問題,你和小明一起回答。
(1)上表反映了哪兩個變量之間的關系?哪個是自變量?哪個是因變量?
(2)如果用h表示距離地面的高度,用t表示溫度,那么隨著h的變化,t是怎么變化的?
(3)你能猜出距離地面6千米的高空溫度是多少嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
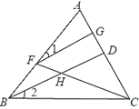
【題目】如圖,已知BD平分∠ABC,點F在AB上,點G在AC上,連接FG、FC,FC與BD相交于點H,如果∠GFH與∠BHC互補.
(1)說明:∠1=∠2.
(2)若∠A=80°,FG⊥AC,求∠ACB的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com