
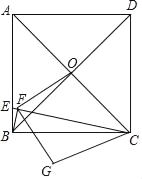
【題目】如圖,正方形ABCD中,AD=4,E在AB上且AB=4BE,連接CE,作BF⊥CE于F,正方形對角線交于O點,連接OF,將△COF沿CE翻折得△CGF,連接BG,則BG的長為_____.
【答案】![]()
【解析】
Rt△BCE中,BF⊥CE,∠CBE=90°,可得BF=![]() =
=![]() ,再判定△COF∽△CEA,可得∠CFO=∠CAB=45°,進而得到∠CFG=∠CFO=45°,∠BFH=90°-45°=45°,可得△BFH是等腰直角三角形,再根據(jù)△COF∽△CEA,可得
,再判定△COF∽△CEA,可得∠CFO=∠CAB=45°,進而得到∠CFG=∠CFO=45°,∠BFH=90°-45°=45°,可得△BFH是等腰直角三角形,再根據(jù)△COF∽△CEA,可得![]() =
=![]() ,即
,即![]() =
=![]() ,進而得出OF=
,進而得出OF=![]() =GF,HG=FG-FH=
=GF,HG=FG-FH=![]() ,最后在Rt△BHG中,由勾股定理可得BG=
,最后在Rt△BHG中,由勾股定理可得BG=![]() =
=![]() .
.
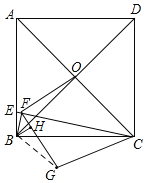
解:如圖,連接BG,過B作BH⊥GF于H,
由題可得,BE=1,BC=4,AE=3,OC=2![]() ,
,
∴Rt△BCE中,CE=![]() ,
,
∵BF⊥CE,∠CBE=90°,
∴BF=![]() =
=![]() ,
,
∵Rt△BCE中,BF⊥CE;Rt△ABC中,BO⊥AC,
∴BC2=CF×CE,BC2=CO×CA,
∴CF×CE=CO×CA,即![]() =
=![]() ,
,
又∵∠OCF=∠ECA,
∴△COF∽△CEA,
∴∠CFO=∠CAB=45°,
由折疊可得,∠CFG=∠CFO=45°,
∴∠BFH=90°-45°=45°,
∴△BFH是等腰直角三角形,
∴FH=BH=![]() BF=
BF=![]() ,
,
∵△COF∽△CEA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴OF=![]() =GF,
=GF,
∴HG=FG-FH=![]() ,
,
∴Rt△BHG中,BG=![]() =
=![]() .
.
故答案為:![]() .
.


 暑假作業(yè)暑假快樂練西安出版社系列答案
暑假作業(yè)暑假快樂練西安出版社系列答案科目:初中數(shù)學 來源: 題型:
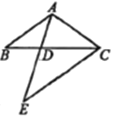
【題目】如圖,在![]() 中,
中,![]() ,將
,將![]() 繞點
繞點![]() 逆時針方向旋轉(zhuǎn)得到
逆時針方向旋轉(zhuǎn)得到![]() ,當點
,當點![]() 落在
落在![]() 邊上時,
邊上時,![]() 的延長線恰好經(jīng)過點
的延長線恰好經(jīng)過點![]() ,則
,則![]() 的長為( )
的長為( )
A. 1B. ![]() C. -1+
C. -1+![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了解永康市某中學八年級學生的視力水平,從中抽查部分學生的視力情況,繪制了如圖統(tǒng)計圖:
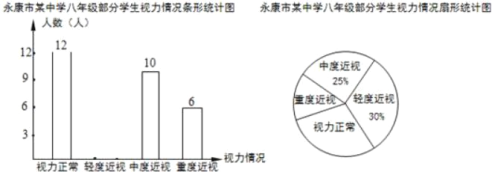
(1)本次調(diào)查的樣本容量是 ;
(2)請補全條形統(tǒng)計圖,并求扇形統(tǒng)計圖中“視力正常”的圓心角度數(shù);
(3)該校八年級共有200位學生,請估計該校八年級視力正常的學生人數(shù).
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
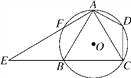
【題目】如圖,已知四邊形ABCD內(nèi)接于⊙O,A是![]() 的中點,AE⊥AC于A,與⊙O及CB的延長線交于點F,E,且
的中點,AE⊥AC于A,與⊙O及CB的延長線交于點F,E,且![]() .
.
(1)求證:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示是一塊含30°,60°,90°的直角三角板,直角頂點O位于坐標原點,斜邊AB垂直x軸,頂點A在函數(shù)y1=![]() (x>0)的圖象上,頂點B在函數(shù)y2=
(x>0)的圖象上,頂點B在函數(shù)y2=![]() (x>0)的圖象上,∠ABO=30°,則
(x>0)的圖象上,∠ABO=30°,則![]() =( )
=( )

A. ﹣![]() B. ﹣
B. ﹣![]() C. ﹣
C. ﹣![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,OA和OB是⊙O的半徑,OB=2,OA⊥OB,P是OA上任一點,BP的延長線交⊙O于點Q,過點Q的⊙O的切線交OA延長線于點R.
(1)求證:RP=RQ;
(2)若OP=PQ,求PQ的長.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知直線l經(jīng)過A(6,0)和B(0,12)兩點,且與直線y=x交于點C,點P(m,0)在x軸上運動.
(1)求直線l的解析式;
(2)過點P作l的平行線交直線y=x于點D,當m=3時,求△PCD的面積;
(3)是否存在點P,使得△PCA成為等腰三角形?若存在,請直接寫出所有符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com