
【題目】某工廠計劃購買![]() ,
,![]() 兩種型號的機器人加工零件.已知
兩種型號的機器人加工零件.已知![]() 型機器人比
型機器人比![]() 型機器人每小時多加工
型機器人每小時多加工![]() 個零件,且
個零件,且![]() 型機器人加工
型機器人加工![]() 個零件用的時間與
個零件用的時間與![]() 型機器人加工
型機器人加工![]() 個零件所用的時間相同.
個零件所用的時間相同.
(1)求![]() ,
,![]() 兩種型號的機器人每小時分別加工多少零件;
兩種型號的機器人每小時分別加工多少零件;
(2)該工廠計劃采購![]() ,
,![]() 兩種型號的機器人共
兩種型號的機器人共![]() 臺,要求每小時加工零件不得少于
臺,要求每小時加工零件不得少于![]() 個,則至少購進
個,則至少購進![]() 型機器人多少臺?
型機器人多少臺?
【答案】(1)![]() 型號機器人每小時加工
型號機器人每小時加工![]() 個零件,
個零件,![]() 型號機器人每小時加工
型號機器人每小時加工![]() 個零件;(2)至少購進
個零件;(2)至少購進![]() 型機器人14臺
型機器人14臺
【解析】
(1)設(shè)B型機器人每小時加工![]() 個零件,則A型機器人每小時加工(x+30)個零件,根據(jù)
個零件,則A型機器人每小時加工(x+30)個零件,根據(jù)![]() 型機器人加工
型機器人加工![]() 個零件用的時間與
個零件用的時間與![]() 型機器人加工
型機器人加工![]() 個零件所用的時間相同建立方程求出其解就可以得出結(jié)論.
個零件所用的時間相同建立方程求出其解就可以得出結(jié)論.
(2)設(shè)至少購進![]() 型機器人
型機器人![]() 臺,根據(jù)每小時加工零件不得少于
臺,根據(jù)每小時加工零件不得少于![]() 個列出不等式并解答.
個列出不等式并解答.
(1)設(shè)B型機器人每小時加工![]() 個零件,則A型機器人每小時加工(x+30)個零件,
個零件,則A型機器人每小時加工(x+30)個零件,
![]()
解得![]()
經(jīng)檢驗![]() 是原方程的解
是原方程的解
當(dāng)x=120時,x+30=150,
答:![]() 型號機器人每小時加工
型號機器人每小時加工![]() 個零件,
個零件,![]() 型號機器人每小時加工
型號機器人每小時加工![]() 個零件;
個零件;
(2)設(shè)至少購進![]() 型機器人
型機器人![]() 臺
臺
![]()
解得![]() ,
,
∵a是整數(shù),
∴a≥14.
答:至少購進![]() 型機器人14臺.
型機器人14臺.


 優(yōu)加精卷系列答案
優(yōu)加精卷系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】東東玩具商店用500元購進一批悠悠球,很受中小學(xué)生歡迎,悠悠球很快售完,接著又用900元購進第二批這種悠悠球,所購數(shù)量是第一批數(shù)量的1.5倍,但每套進價多了5元.
(1)求第一批悠悠球每套的進價是多少元;
(2)如果這兩批悠悠球每套售價相同,且全部售完后總利潤不低于25%,那么每套悠悠球的售價至少是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】春節(jié)前,某超市從廠家購進某商品,已知該商品每個的成本價為30元,經(jīng)市場調(diào)查發(fā)現(xiàn),該商品每天的銷售量![]() (個)與銷售單價
(個)與銷售單價![]() (元) 之間滿足一次函數(shù)關(guān)系,當(dāng)該商晶每個售價為40元時,每天可賣出300個;當(dāng)該商晶每個售價為60元時,每天可賣出100個.
(元) 之間滿足一次函數(shù)關(guān)系,當(dāng)該商晶每個售價為40元時,每天可賣出300個;當(dāng)該商晶每個售價為60元時,每天可賣出100個.
(1)![]() 與
與![]() 之間的函數(shù)關(guān)系式為__________________(不要求寫出
之間的函數(shù)關(guān)系式為__________________(不要求寫出![]() 的取值范圍) ;
的取值范圍) ;
(2)若超市老板想達到每天不低于220個的銷售量,則該商品每個售價定為多少元時,每天的銷售利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如下圖1,將三角板放在正方形![]() 上,使三角板的直角頂點
上,使三角板的直角頂點![]() 與正方形
與正方形![]() 的頂點
的頂點![]() 重合,三角板的一邊交
重合,三角板的一邊交![]() 于點
于點![]() .另一邊交
.另一邊交![]() 的延長線于點
的延長線于點![]() .
.
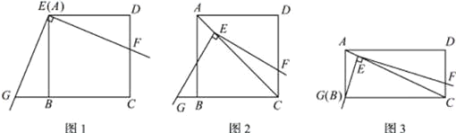
(1)觀察猜想:線段![]() 與線段
與線段![]() 的數(shù)量關(guān)系是 ;
的數(shù)量關(guān)系是 ;
(2)探究證明:如圖2,移動三角板,使頂點![]() 始終在正方形
始終在正方形![]() 的對角線
的對角線![]() 上,其他條件不變,(1)中的結(jié)論是否仍然成立?若成立,請給予證明:若不成立.請說明理由:
上,其他條件不變,(1)中的結(jié)論是否仍然成立?若成立,請給予證明:若不成立.請說明理由:
(3)拓展延伸:如圖3,將(2)中的“正方形![]() ”改為“矩形
”改為“矩形![]() ”,且使三角板的一邊經(jīng)過點
”,且使三角板的一邊經(jīng)過點![]() ,其他條件不變,若
,其他條件不變,若![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
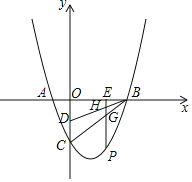
【題目】已知拋物線y=x2﹣2x﹣3與x軸交于點A、B,與y軸交于點C,點D為OC中點,點P在拋物線上.
(1)直接寫出A、B、C、D坐標(biāo);
(2)點P在第四象限,過點P作PE⊥x軸,垂足為E,PE交BC、BD于G、H,是否存在這樣的點P,使PG=GH=HE?若存在,求出點P坐標(biāo);若不存在,請說明理由.
(3)若直線y=![]() x+t與拋物線y=x2﹣2x﹣3在x軸下方有兩個交點,直接寫出t的取值范圍.
x+t與拋物線y=x2﹣2x﹣3在x軸下方有兩個交點,直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖像在第一象限有一個公共點,其橫坐標(biāo)為1,則一次函數(shù)
的圖像在第一象限有一個公共點,其橫坐標(biāo)為1,則一次函數(shù)![]() 的圖像可能是( )
的圖像可能是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在一個不透明的布袋中,有![]() 個紅球,
個紅球,![]() 個白球,這些球除顏色外都相同.
個白球,這些球除顏色外都相同.
(1)攪勻后從中任意摸出![]() 個球,摸到紅球的概率是________;
個球,摸到紅球的概率是________;
(2)攪勻后先從中任意摸出![]() 個球(不放回),再從余下的球中任意摸出
個球(不放回),再從余下的球中任意摸出![]() 個球.求兩次都摸到紅球的概率.(用樹狀圖或表格列出所有等可能出現(xiàn)的結(jié)果)
個球.求兩次都摸到紅球的概率.(用樹狀圖或表格列出所有等可能出現(xiàn)的結(jié)果)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣1,給出下列結(jié)論:
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正確的個數(shù)有( )

A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
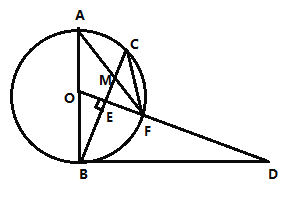
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 為
為![]() 上一點,
上一點,![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() 為
為![]() 延長線上一點,且
延長線上一點,且![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)求證:![]() ;
;
(3)若![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com