
【題目】如圖,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,點(diǎn)E、F分別從B、C兩點(diǎn)同時出發(fā),其中點(diǎn)E沿BC向終點(diǎn)C運(yùn)動,速度為4cm/s;點(diǎn)F沿CA、AB向終點(diǎn)B運(yùn)動,速度為5cm/s,設(shè)它們運(yùn)動的時間為x(s).
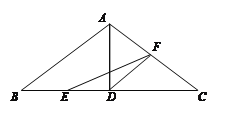
(1)求x為何值時,△EFC和△ACD相似;
(2)是否存在某一時刻,使得△EFD被 AD分得的兩部分面積之比為3:5,若存在,求出x的值,若不存在,請說明理由;
(3)若以EF為直徑的圓與線段AC只有一個公共點(diǎn),求出相應(yīng)x的取值范圍.
【答案】(1)![]()
(2)不存在.
(3)![]()
【解析】分析:(1)點(diǎn)F在AC上,點(diǎn)E在BD上時,①當(dāng)![]() 時,△CFE∽△CDA,②當(dāng)
時,△CFE∽△CDA,②當(dāng)![]() 時,分別列出方程求解即可;
時,分別列出方程求解即可;
(2)不存在.分兩種情形說明:如圖2中,當(dāng)點(diǎn)F在AC上,點(diǎn)E在BD上時,作FH⊥BC于H,EF交AD于N.只要證明EN=FN即可解決問題;
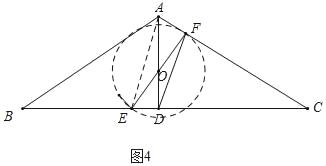
(3)分四種情形①如圖3中,當(dāng)以EF為直徑的⊙O經(jīng)過點(diǎn)A時,⊙O與線段AC有兩個交點(diǎn),連接AE,則∠EAF=90°.②如圖4中,當(dāng)⊙O與AC相切時,滿足條件,此時t=![]() .③如圖5中,當(dāng)⊙O與AB相切時,④如圖6中,⊙O經(jīng)過點(diǎn)A時,連接AE,則∠EAF=90°.分別求解即可.
.③如圖5中,當(dāng)⊙O與AB相切時,④如圖6中,⊙O經(jīng)過點(diǎn)A時,連接AE,則∠EAF=90°.分別求解即可.
詳解:(1)如圖1中,
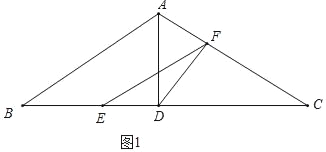
點(diǎn)F在AC上,點(diǎn)E在BD上時,①當(dāng)![]() 時,△CFE∽△CDA,
時,△CFE∽△CDA,
∴![]() =
=![]() ,
,
∴t=![]() ,
,
②當(dāng)![]() 時,即
時,即![]() =
=![]() ,
,
∴t=2,
當(dāng)點(diǎn)F在AB上,點(diǎn)E在CD上時,不存在△EFC和△ACD相似,
綜上所述,t=![]() s或2s時,△EFC和△ACD相似.
s或2s時,△EFC和△ACD相似.
(2)不存在.
理由:如圖2中,當(dāng)點(diǎn)F在AC上,點(diǎn)E在BD上時,作FH⊥BC于H,EF交AD于N.
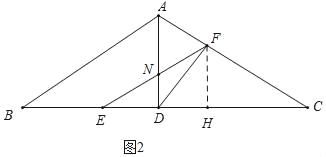
∵CF=5t.BE=4t,
∴CH=CFcosC=4t,
∴BE=CH,
∵AB=AC,AD⊥BC,
∴BD=DC,
∴DE=DH,
∵DN∥FH,
∴![]() =1,
=1,
∴EN=FN,
∴S△END=S△FND,
∴△EFD被 AD分得的兩部分面積相等,
同法可證當(dāng)點(diǎn)F在AB上,點(diǎn)E在CD上時,△EFD被 AD分得的兩部分面積相等,
∴不存在某一時刻,使得△EFD被 AD分得的兩部分面積之比為3:5.
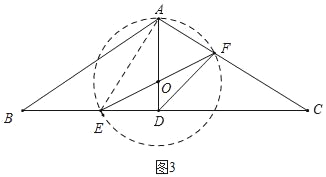
(3)①如圖3中,當(dāng)以EF為直徑的⊙O經(jīng)過點(diǎn)A時,⊙O與線段AC有兩個交點(diǎn),連接AE,則∠EAF=90°.
由![]() =cosC=
=cosC=![]() ,可得
,可得![]() =
=![]() ,
,
∴t=![]() ,
,
∴0≤t<![]() 時,⊙O與線段AC只有一個交點(diǎn).
時,⊙O與線段AC只有一個交點(diǎn).
②如圖4中,當(dāng)⊙O與AC相切時,滿足條件,此時t=![]() .
.
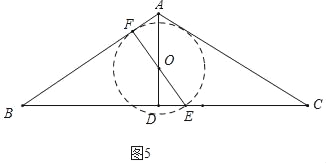
③如圖5中,當(dāng)⊙O與AB相切時,cosB=![]() ,即
,即![]() =
=![]() ,解得t=
,解得t=![]() .
.
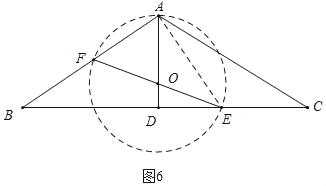
④如圖6中,⊙O經(jīng)過點(diǎn)A時,連接AE,則∠EAF=90°.
由cosB=![]() =
=![]() ,即
,即![]() =
=![]() ,t=
,t=![]() ,
,
∴![]() <t≤4時,⊙O與線段AC只有一個交點(diǎn).
<t≤4時,⊙O與線段AC只有一個交點(diǎn).
綜上所述,當(dāng)⊙O與線段AC只有一個交點(diǎn)時,0≤t<![]() 或
或![]() 或
或![]() 或
或![]() <t≤4.
<t≤4.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某市水果批發(fā)部門欲將A市的一批水果運(yùn)往本市銷售,有火車和汽車兩種運(yùn)輸方式,運(yùn)輸過程中的損耗均為200元/時。其它主要參考數(shù)據(jù)如下:
運(yùn)輸工具 | 途中平均速度(千米/時) | 運(yùn)費(fèi)(元/千米) | 裝卸費(fèi)用(元) |
火車 | 100 | 15 | 2000 |
汽車 | 80 | 20 | 900 |
(1)如果汽車的總支出費(fèi)用比火車費(fèi)用多1100元,你知道本市與A市之間的路程是多少千米嗎?請你列方程解答.
(2)如果A市與某市之間的距離為S千米,且知道火車與汽車在路上耽誤的時間分別為2小時和3.1小時,你若是某市水果批發(fā)部門的經(jīng)理,要將這種水果從A市運(yùn)往本市銷售。你將選擇哪種運(yùn)輸方式比較合算呢?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一個點(diǎn)從數(shù)軸上的原點(diǎn)開始,先向右移動1個單位長度,再向左移動2個單位長度,再向右移動3個單位長度,再向左移動4個單位長度,……,移動2019次后,該點(diǎn)所對應(yīng)的數(shù)是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)y=ax2-8ax(a<0)的圖像與x軸的正半軸交于點(diǎn)A,它的頂點(diǎn)為P.點(diǎn)C為y軸正半軸上一點(diǎn),直線AC與該圖像的另一交點(diǎn)為B,與過點(diǎn)P且垂直于x軸的直線交于點(diǎn)D,且CB:AB=1:7.
(1)求點(diǎn)A的坐標(biāo)及點(diǎn)C的坐標(biāo)(用含a的代數(shù)式表示);
(2)連接BP,若△BDP與△AOC相似(點(diǎn)O為原點(diǎn)),求此二次函數(shù)的關(guān)系式.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校為了了解學(xué)生孝敬父母的情況(選項:A為父母洗一次腳;B幫父母做一次家務(wù);C給父母買一件禮物;D其它),在全校范圍內(nèi)隨機(jī)抽取了若干名學(xué)生進(jìn)行調(diào)查,得到如下圖表(部分信息未給出):
根據(jù)以上信息解答下列問題:


(1)這次被調(diào)查的學(xué)生有多少人?
(2)求表中m,n,p的值,并補(bǔ)全條形統(tǒng)計圖.
(3)該校有1600名學(xué)生,估計該校全體學(xué)生中選擇B選項的有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,點(diǎn)![]() 為坐標(biāo)原點(diǎn),正方形
為坐標(biāo)原點(diǎn),正方形![]() 與長方形
與長方形![]() 的位置如圖所示,點(diǎn)
的位置如圖所示,點(diǎn)![]() 在
在![]() 軸的正半軸上,點(diǎn)
軸的正半軸上,點(diǎn)![]() 在
在![]() 軸的正半軸上,點(diǎn)
軸的正半軸上,點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 在
在![]() 軸的負(fù)半軸上(點(diǎn)
軸的負(fù)半軸上(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的右側(cè)),點(diǎn)
的右側(cè)),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,![]() ,實數(shù)
,實數(shù)![]() ,
,![]() 的值滿足
的值滿足![]() .
.
(1)求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)長方形![]() 以每秒1個單位長度的速度向右平移
以每秒1個單位長度的速度向右平移![]() (
(![]() )秒得到矩形
)秒得到矩形![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() 分別為點(diǎn)
分別為點(diǎn)![]() ,
,![]() ,
,![]() ,
,![]() 平移后的對應(yīng)點(diǎn),設(shè)矩形
平移后的對應(yīng)點(diǎn),設(shè)矩形![]() 與正方形
與正方形![]() 重合部分的面積為
重合部分的面積為![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并直接寫出相應(yīng)的
,并直接寫出相應(yīng)的![]() 的范圍;
的范圍;
(3)在(2)的條件下,在長方形![]() 出發(fā)運(yùn)動的同時,點(diǎn)
出發(fā)運(yùn)動的同時,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿正方形的邊以每秒2個單位長度的速度順時針方向運(yùn)動(即
出發(fā),沿正方形的邊以每秒2個單位長度的速度順時針方向運(yùn)動(即![]() ),連接
),連接![]() ,
,![]() ,當(dāng)三角形
,當(dāng)三角形![]() 的面積為15時,求
的面積為15時,求![]() 時相應(yīng)的
時相應(yīng)的![]() 值,并直接寫出此時刻
值,并直接寫出此時刻![]() 值及點(diǎn)
值及點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】初二年級教師對試卷講評課中學(xué)生參與的深度與廣度進(jìn)行評價調(diào)查,其評價項目為主動質(zhì)疑、獨(dú)立思考、專注聽講、講解題目四項.評價組隨機(jī)抽取了若干名初二學(xué)生的參與情況,繪制成如圖所示的頻數(shù)分布直方圖和扇形統(tǒng)計圖(均不完整),請根據(jù)圖中所給信息解答下列問題:
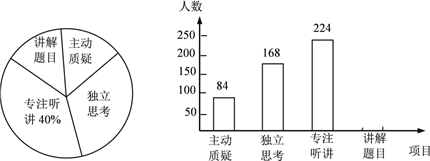
(1)在這次評價中,一共抽查了 名學(xué)生;
(2)在扇形統(tǒng)計圖中,項目“主動質(zhì)疑”所在的扇形的圓心角的度數(shù)為 度;
(3)請將頻數(shù)分布直方圖補(bǔ)充完整;
(4)如果全市有6000名初二學(xué)生,那么在試卷評講課中,“獨(dú)立思考”的初二學(xué)生約有多少人?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com